1. 서 론

모멘트골조는 기둥과 보로 이루어진 구조시스템이다. 이는 전단벽, 가새 등이 사용된 다른 구조시스템과 비교하여 건축 계획적 다양성이 뛰어난 장점을 가진다. 강진으로 인한 지반 진동 시, 복합적인 변형을 통한 건물 진동의 결과로써 발생하는 휨, 축력, 전단 작용에 저항하도록 골조의 보, 기둥, 보-기둥 접합부 등이 설계된다. 특별한 설계 및 상세 요구조건은 강성이나 강도의 심각한 손실 없이 골조가 강진에 저항이 가능하도록 한다. 중간모멘트골조와 보통모멘트골조와 비교하여 내진 성능을 향상시키는 추가 요구조건들을 만족하는 이러한 모멘트저항골조를 특수모멘트골조라고 한다(Hamburger et al., 2009; Moehle et al., 2008).

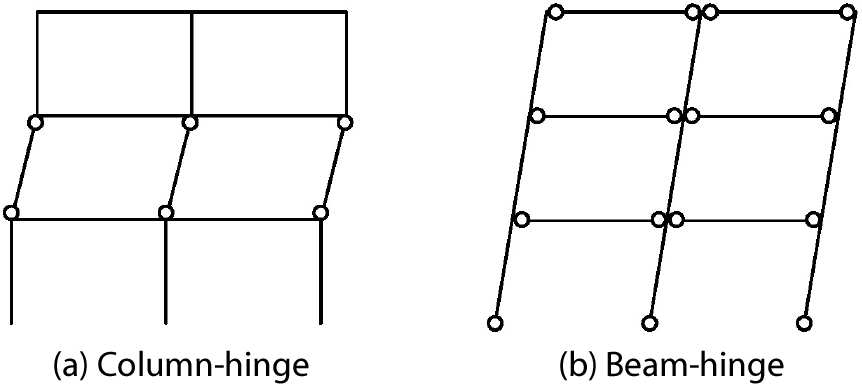
모멘트골조는 기둥과 보의 강도비, 강성비 등에 따라서 힘의 거동이 달라지게 된다. Fig. 1(a)와 같이 특정 층의 기둥 강도가 낮아 해당 층에서 소성힌지가 집중하여 발생하게 되면 변형이 크게 발생하면서 저항능력이 저하된다. 따라서 구조물의 연성 능력을 증대하기 위해서는 소성힌지가 구조물 전체에 걸쳐 고르게 발생하도록 유도하는 것이 중요하다. 이와 같은 이유로 Fig. 1(b)와 같이 보-힌지 붕괴모드를 유도하여 지진에 의한 피해를 감소시키는 전략이 권장되고 있다.

Fig. 1.

Collapse mode

ACI 318-19(ACI Committee 318, 2019)는 철근콘크리트 특수모멘트골조의 경우 ‘강기둥-약보(Strong Column-Weak Beam)’ 조건을 추가적으로 만족하도록 제시하고 있다. 이는 기둥은 상대적으로 강하게 설계하고 보는 약하게 설계하여 기둥보다 보에서 먼저 소성힌지가 발생시키는 목적을 가진다. 이를 위해 연결부에서 기둥의 휨강도 합이 보의 휨강도 합보다 크도록 하고 있다. ACI 318-19는 기둥-보 휨강도비가 ‘1.2’ 이상이 되도록 제시하고 있다.

그러나 ‘강기둥-약보’ 조건을 만족하더라도 보-힌지 붕괴모드가 유도되지 않을 수 있다. 이는 ‘강기둥-약보’ 조건이 선형정적해석이라는 가정에 근거하고 있기 때문이다. 선형정적해석의 경우 횡하중에 의한 기둥의 휨모멘트 분포는 Fig. 2(a)와 같이 기둥의 중앙 부근에서 부호가 바뀐다고 가정할 수 있고, 그래서 연결부에서 기둥의 휨강도 합은 보의 휨강도 합과 같다고 할 수 있다. 그러나 동적해석 또는 비선형해석을 하게 되면 고차모드 또는 모멘트 재분배 등으로 인해 위의 가정이 성립되지 않고 Fig. 2(b)와 같이 부재의 휨모멘트 분포가 달라지는 경우가 발생할 수 있다. 이렇게 되면 연결부에서 기둥의 한 단부 휨강도가 나머지 부재 단부의 휨강도 합과 일치해야 하는 상황이 발생하여 기둥을 보보다 강하게 설계하더라도 먼저 소성힌지가 발생하면서 보-힌지 붕괴모드가 유도되지 않을 수 있다(Kuntz and Brouning, 2003; Park and Paulay, 1975).

Fig. 2.

Comparison of moment distributions

모멘트골조의 보-힌지 붕괴모드를 유도하기 위해 여러 방법이 제시되었다. Lee(1996)은 비선형정적해석을 분석하여 붕괴 시점에서 하부기둥의 휨모멘트가 상부기둥의 휨모멘트보다 3배 정도임을 확인하고 이를 근거로 하여 하부기둥의 휨강도가 해당 기둥에 연결되는 보 휨강도 합의 75% 이상이 되어야 한다는 설계식을 제시하였다. Nakashima와 Sawaizumi(2000)은 여러 조건에 대한 비선형시간이력해석을 수행하여 기둥이 탄성상태를 유지하기 위해 요구되는 기둥-보 휨강도비를 분석하였다. 지진 수준에 따라 다르지만 최소 1.5 이상이 되어야 하는 것으로 나타났다. Dooley와 Bracci(2001)는 여러 기둥-보 휨강도비(0.8~2.4) 조건에 따라 설계된 3층, 6층 예제에 시간이력해석을 적용하여 기둥에서 소성거동이 나타나지 않기 위한 휨강도비를 분석하였다. 그 결과 휨강도비가 ‘2.0’ 이상은 되어야 적절하게 기둥이 탄성상태를 유지할 수 있는 것으로 제시하였다. Kuntz와 Brouning(2003)은 모든 절점에 동일한 휨강도비를 적용하는 기존 방법으로는 보-힌지 붕괴모드를 유도하는데 부적절하며, 상부층 보의 휨강도를 낮추어 설계하는 방법이 기둥의 힌지 발생을 감소시키는데 효과적이라고 제안하였다. Medina와 Krawinkler(2005)는 지진수준, 구조물 고유주기, 층수 등을 변수로 하여 모멘트골조 기둥의 거동 영향을 분석하였다. 기존 강기둥-약보 조건만으로는 기둥의 탄성상태를 유지하기 어려워 보다 강화된 조건이 필요하다고 제시하였다. 또한, 기둥의 요구 휨강도는 지진수준과 고유주기와 관련이 있지만, 층수에 의한 영향은 적은 것으로 나타났다.

Park과 Choi(2016)은 철골모멘트골조의 보-힌지 붕괴 모드를 유도하기 위한 유전자알고리즘을 이용한 최적내진설계기법을 제시하였다. 본 연구는 이에 대한 후속으로 대상 구조물을 다르게 하여 철근콘크리트 모멘트골조의 보-힌지 붕괴 모드를 유도하기 위한 최적내진설계기법을 제시한다. 이는 유전자알고리즘(Choi et al., 2010)을 사용하며, 기둥의 소성힌지 발생을 억제하는 제약조건을 설정하여 보-힌지 붕괴모드를 유도한다. 강도설계를 위해 고정하중, 활하중, 지진하중에 대한 선형정적해석이 수행되고, 소성힌지 및 비선형거동 특성을 파악하기 위해 비선형정적해석이 수행된다. 이러한 구조해석을 위해 OpenSees(Mazzoni et al., 2006)를 사용한다. 이 기법을 4층 철근콘크리트 모멘트골조 예제에 적용하여 제안된 기법을 검증한다. 예제 적용을 통해 철근콘크리트 모멘트골조의 보-힌지 붕괴모드를 유도하기 위해 요구되는 기둥-보 강도비를 분석한다.

2. 최적내진설계기법

2.1 유전자알고리즘

본 연구에서는 최적화기법으로 유전자알고리즘(Getnetic Algorithm)을 사용한다. 이는 다윈의 진화론 원리를 이용한 방법이다. 이는 설계안을 의미하는 개체(Individual)로 이루어진 개체군(Population)에서 환경 적합도가 높은 개체가 높은 확률로 살아남을 수 있으며, 교배(Crossover), 돌연변이(Mutation) 등을 통해 다음 세대(Generation)에 유전 정보를 전달할 수 있다고 가정한다. 설계안의 설계변수는 개체의 유전 정보를 의미한다. 유전자 알고리즘은 다수의 개체들로 이루어진 해 집단을 여러 세대에 걸쳐 비교 및 평가하면서 더 좋은 목적함수를 가지는 개체들로 진화시킨다. 이 방법은 다양한 문제에 적용하기 쉽고, 전역 해의 탐색능력이 우수하여 공학분야에서 널리 사용되고 있다.

한편, 현실적으로 최적화 문제는 가격과 성능처럼 서로 상충되는 두 가지 이상의 목적함수를 동시에 고려할 필요가 있다. 그래서 본 연구에서는 Deb 등(2002)이 제안한 다목적 최적화 기법인 Non-dominated Sorting Genetic Algorithm-II(NSGA-II)를 이용한다. NSGA-II는 각 개체의 목적함수 및 제약조건을 평가하고 이에 근거하여 각 개체 간의 지배(Dominance) 관계, 순위(Rank), 군집도 거리(Crowding distance) 등을 계산하게 된다. 이 값을 통해 각 개체의 적합도가 정해지며 다음 세대로의 선별(Selection) 과정에 활용된다. Fig. 3은 본 연구에서 제안하는 최적내진설계기법의 흐름도를 나타낸다.

Fig. 3.

Flow chart of the proposed optimal seismic design method

2.2 목적함수

본 논문에서 두 가지의 목적함수를 사용한다. 첫 번째 목적함수는 경제성을 고려하기 위해서 RC 모멘트골조의 구조 비용을 최소화하는 것이며, 두 번째 목적함수는 비선형해석을 통해 얻게 되는 최상층 횡변위-밑면전단력 그래프를 통해 계산되는 에너지 소산량를 최대화하는 것이다. 에너지 소산량을 최대화하기 위해 그 값을 역수로 하고 이를 최소화하도록 하였다. 두 번째 목적함수를 사용한 이유는 구조물의 성능을 고려하는 것이다. 첫 번째와 두 번째 목적 함수는 식 (1), (2)와 같다.

여기서, ConcCosti과 RebarCosti는 각각 ith 부재에 사용된 콘크리트 비용과 철근 비용을 의미한다. 기둥에 사용된 철근의 길이는 기둥의 길이와 동일하며, 보에 사용된 철근 길이는 보의 단부와 중앙부로 구분하여 길이를 산정하도록 한다. 보의 단부와 중앙부에 설치되는 철근의 길이는 각각 보 길이의 1/3로 가정한다. Areapushover은 비선형 정적 해석을 통해 얻은 최상층 변위-밑면 전단력 그래프의 면적이며, 이는 구조물의 에너지 소산량을 의미한다. 그래프의 면적을 최대화하면 초기강성뿐만 아니라 연성능력이 뛰어난 설계안을 유도할 수 있다.

2.3 제약조건

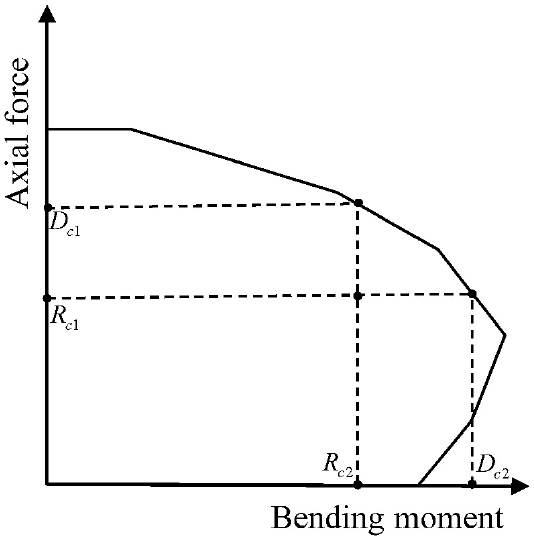
철근콘크리트 기둥의 강도 검토는 Fig. 4의 P-M 상관도를 이용한다. 본 연구에서는 구조해석을 통해 얻게 되는 ith 기둥의 소요축력 Rc1i과 소요모멘트 Rc2i를 구하고, 이를 기반으로 하여 설계축력 Dc1i과 설계모멘트 Dc2i를 결정한다. 이를 통해 식 (3), (4)와 같이 기둥의 축강도와 휨강도에 관한 제약 조건이 사용된다.

보의 휨 강도에 관한 제약 조건이 식 (5)와 같이 사용된다. Rbi와 Dbi은 각각 ith 보 부재의 소요강도와 설계강도이다.

기둥-보 접합부의 휨강도비 제약조건이 식 (6)와 같이 사용된다. ∑Mnb와 ∑Mnc는 ith 접합부에서 각각 보의 휨강도의 합과 기둥의 휨강도의 합이다.

철근콘크리트 모멘트골조의 보-힌지 붕괴 기구를 유도하기 위해 식 (7)이 사용된다.

여기서, Nh,c은 기둥 단부에서 발생한 소성 힌지의 개수이며, Njoint은 고려한 접합부 개수이다. 이 제약 조건을 통해 구조물은 최상층의 접합부를 제외한 기둥의 접합부에서 소성 힌지가 발생하지 않는 설계안을 얻도록 한다. 최상층의 기둥 접합부는 이 제약조건에서 고려되지 않는다. 이는 최상층의 기둥 접합부에서의 소성 힌지는 구조물의 전체 거동에 큰 영향을 미치지 않기 때문이다.

Fig. 4.

P-M interaction diagram

이 밖에 기둥의 시공성을 고려하기 위하여 수직으로 연속된 기둥의 단면과 철근 개수에 관한 제약조건을 고려하였다. 이는 수직으로 연속된 기둥 중에서 아래 기둥의 단면 크기가 위 기둥의 단면보다 크거나 같도록 한다. 또한 아래 기둥의 철근 개수도 위 기둥의 철근 개수보다 크거나 같도록 제약한다. 이와 같은 기둥의 시공성에 관한 제약은 다른 제약 조건처럼 제약식을 이용하여 각 개체마다 평가하는 대신, 각 개체의 설계변수 값을 배당할 때 정렬 함수를 이용하여 아래에 위치하는 설계변수 값이 위의 설계변수 값보다 상대적으로 크거나 같도록 하였다. 이로써, 모든 개체에 배당된 설계변수 값은 기둥의 시공성 제약을 만족시키도록 하여 추가적인 제약식을 고려하지 않는다.

3. 제안 기법 검증 시뮬레이션

3.1 해석 모델 개요

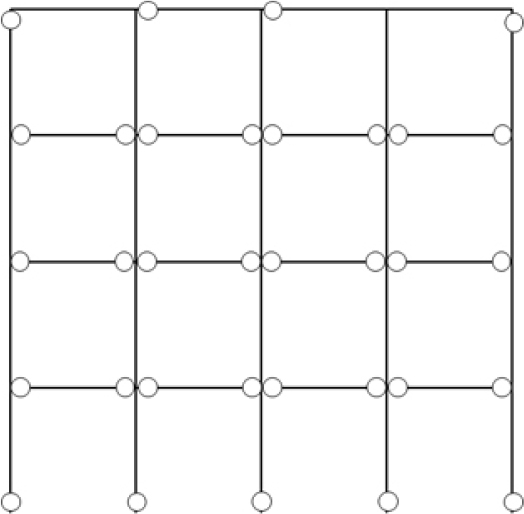
제안하는 최적내진설계기법은 Fig. 5와 같은 4층 4경간 예제에 적용되었다. OpenSees가 구조해석을 위해 사용된다. 콘크리트와 철근의 재료강도는 각각 35MPa와 420MPa이다. 구조물의 강도 조건을 검토하기 위하여 선형 정적해석을 수행하며, 구조물의 힌지 제약조건과 에너지 소산량을 평가하기 위하여 비선형 정적해석을 수행한다. 비선형 정적해석은 역삼각형 패턴을 사용하며, 최상층의 횡변위에 기반한 변위제어를 수행한다. 초기 목표 변위는 최상층의 횡변위가 구조물 전체 높이의 5%으로 설정한다. 참고로 FEMA 356(2000)에서 제시하는 붕괴 수준에 해당하는 층간변위 수준은 구조물의 높이의 4%이다. 그래서 목표변위에 이르렀을 때는 이미 붕괴기구가 형성되었다고 가정한다. OpenSees의 elasticBeamColumn와 beam WithHinges요소를 사용하여 모델링한다. beamWithHinges요소는 부재의 소성거동이 부재의 양단에서만 발생한다고 가정한다. 패널존 변형은 고려하지 않으며, center-line 모델을 사용한다. P-delta 효과가 고려되며, 부재의 강도 및 강성 저하는 고려되지 않는다.

Fig. 5.

Elevation of an example structure

본 연구에서 사용된 기둥과 보의 그룹 수는 Fig. 5와 같다. 기둥은 내부와 외부 기둥을 구분하며, 각각을 층별로 구분하여 총 8개의 그룹으로 나누어진다. 보는 층별로 구분하여 총 4개의 그룹으로 나누어진다. 기둥과 보의 단면을 정의하는 설계변수는 Fig. 6과 같이 각각 3개(단면 치수, 철근 지름, 철근 개수)와 4개(단면 폭, 단면 깊이, 철근 지름, 철근 개수)이다. 따라서 기둥과 보에 사용된 설계변수는 각각 24개와 16개이다.

Fig. 6.

Types of design variables for columns and beams

같은 층에 위치한 보의 i단과 j단의 철근 배근은 동일한 것으로 가정하며, 압축철근비는 인장철근비의 50%으로 가정한다 (Hajirasouliha et al., 2012). 만약 인장철근의 개수가 홀수이면 1을 더한 후 2로 나눈 값을 압축철근의 개수로 정한다. 압축 및 인장철근은 최소 및 최대 철근비, 최소 철근 간격을 만족하는 범위 내에서 결정되도록 한다.

기둥의 단면은 정사각형으로 한정해서 기둥의 폭이 정해지면 기둥의 단면이 정해지는 것으로 한다. 보의 단면은 정방형으로 한정한다. 보의 폭이 정해지면, 보의 깊이는 정해진 보의 폭의 1.5배부터 2.5배 사이의 값을 가지도록 한다. 기둥과 보의 단면치수는 50mm씩 변화하는 것으로 가정한다. 기둥과 보의 설계변수 범위는 Table 1과 같다.

철골모멘트골조의 최적화에서는 기성 단면을 사용한 반면, 철근콘크리트 모멘트골조의 최적화에서는 단면을 정할 때 부재 치수, 철근 수량 등을 조합해야 하기 때문에 상대적으로 많은 설계변수가 사용된다. 이는 해 탐색 능력을 저하시켜 소요 시간을 증가시키게 된다. 그래서 소요 계산 시간을 줄이기 위해 멀티코어를 활용한 병렬해석을 함께 수행한다.

3.2 시뮬레이션 결과 분석

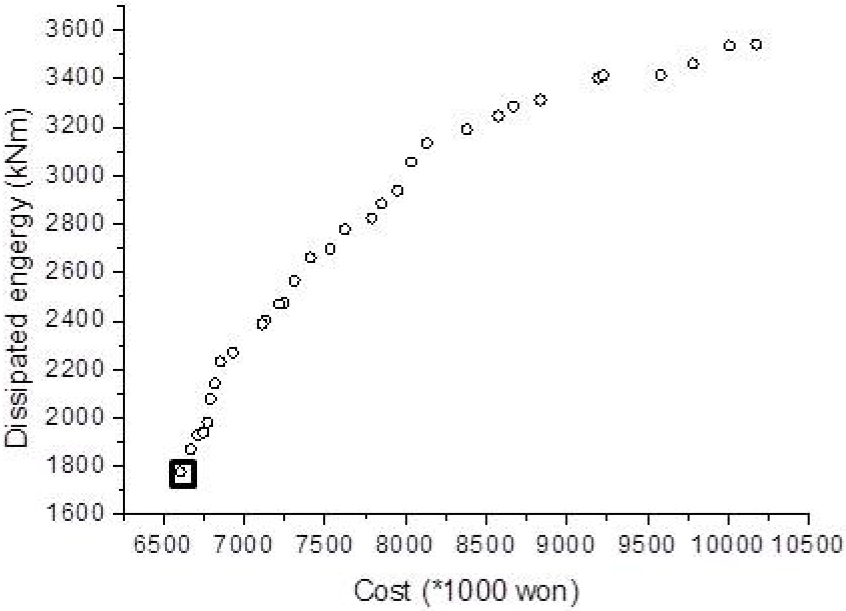
제안한 기법을 적용한 결과 Fig. 7과 같은 40개의 비지배해를 얻었다. 구조 비용이 증가할수록 소산에너지가 증가하는 것을 확인할 수 있다. 즉 에너지소산량 같은 구조적 성능을 높이기 위해서는 비용이 증가하는 것을 확인할 수 있다. 두 번째 목적함수에 첫 번째 목적함수를 나누어 단위 비용당 소산에너지량을 평가하였고, 이 중에서 가장 큰 설계안을 선택하였다. 그 결과는 Fig. 7에서 표시된 비지배해 중에서 비용이 가장 작은 설계안이 선택되었다.

Fig. 7.

Optimal solution distribution obtained by applying the proposed method

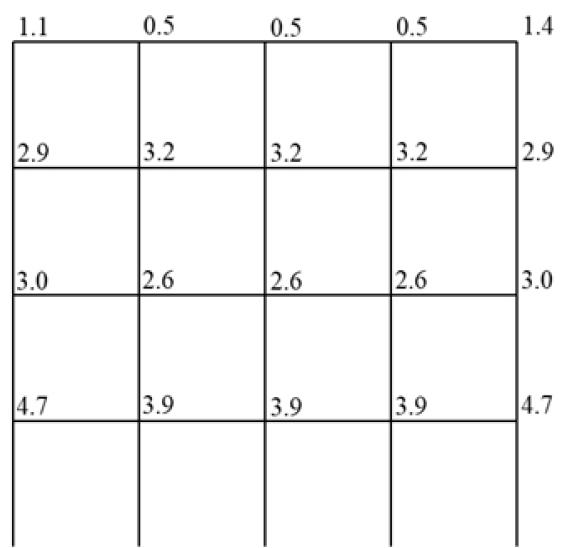
본 연구에서 제시하는 최적화 기법은 최상층의 접합부를 제외한 모든 접합부의 보 단부에서만 소성힌지가 발생하도록 하였는데, 이는 선택된 해의 소성힌지 분포를 나타내는 Fig. 8을 통해 검증할 수 있다. 최상층 단부와 지점을 제외한 모든 기둥 단부에서는 소성힌지가 발생하지 않았으며, 최상층을 제외한 모든 층의 보에서 소성힌지가 고르게 발생한 것으로 나타났다. 제안하는 기법이 보-힌지 붕괴 모드를 적절하게 유도하고 있음을 확인할 수 있다.

Fig. 8.

Plastic hinge distribution for the selected solution

Fig. 9에 나타난 숫자는 각 접합부의 기둥-보 휨강도비를 의미한다. 제약조건으로 고려된 모든 접합부의 휨강도비가 ACI 318-19에서 제시하고 있는 ‘1.2’보다 큰 것을 확인할 수 있다. 기둥이 탄성상태를 유지하기 위해서는 기준에서 제시하는 값보다 더 큰 휨강도비가 요구된다는 점은 기존 연구결과(Lee, 1996; Medina and Krawinkler, 2005; Nakashima and Sawaizumi, 2000; Park and Choi, 2016)와 동일하다.

Fig. 9.

Column-to-beam flexural strength ratio for the selected solution

단일 코어를 사용하여 알고리즘을 수행한 전체 소요 시간은 59,694.20초이다. 이 중에서 함수를 호출하는데 소요된 시간은 8.82초(약 0.01%)이며, 구조해석에 소요된 시간은 59,685.38초(약99.99%)이다. 이를 코어 2개와 4개로 각각 구분하여 수행할 경우 소요시간이 각각 33,487.73초, 23,725.81초로 나타났다. 사용하는 코어의 수를 증가시키면 소요시간은 효과적으로 감소하는 것으로 나타났다. 그러나 식 (8)을 이용하여 코어의 효율을 계산하면 코어 2개와 4개에 대한 효율은 각각 89.13%, 62.90%로 감소하는 것으로 나타났다. 이것은 각 코어에서 균등하게 개체의 구조해석을 수행하였기 때문에 코어의 수가 증가할수록 개체 간의 구조해석 수행시간이 차이가 발생하고 그 만큼 코어가 대기하는 시간이 증가하기 때문으로 판단된다.

4. 결 론

본 연구에서는 철근콘크리트 모멘트골조의 보-힌지 붕괴를 유도하기 위한 유전자알고리즘 기반의 최적내진설계기법을 제시하였다. 이는 비선형정적해석을 통해 보와 연결되는 기둥 단부의 소성힌지 발생 여부를 조사하고, 소성힌지가 발생하였을 경우 제약조건을 위배하도록 하는 방법을 사용하였다. 제약조건을 만족시키지 못하는 개체보다 만족시키는 개체가 다음 세대에 살아남을 확률을 높게 하여 최적해를 찾아가도록 하였다. 제안하는 기법을 4층 예제 구조물에 적용하였으며, 그 결과 보-힌지 붕괴 기구가 유도됨을 확인하였다.

보-힌지 붕괴 모드가 유도되는 설계안의 기둥-보 휨강도비는 ACI 318-19 등에서 제시되는 조건보다 더 큰 값을 가지며 절점 위치에 따라 값의 차이가 있는 것으로 나타났다. 이는 Kuntz와 Brouning(2003)이 언급한 것처럼 현실적으로 모든 절점에 동일한 휨강도비 조건을 적용하여 기둥의 탄성 상태를 유지하는 것은 어렵다고 판단된다.

유전자알고리즘은 다수의 개체를 운영하여 해를 탐색하기 때문에 소요시간을 줄이기 위해 병렬해석을 적용하기에 적합하다. 본 연구에서는 개체의 평가 과정에서 비선형정적해석을 수행해야 했기 때문에 알고리즘을 실행하는데 약 16시간이 소요되었다. 이러한 긴 시간은 제안하는 기법의 적용성을 떨어뜨리기 때문에 개선방법으로 멀티코어를 활용한 병렬해석을 수행하여 소요시간을 감소시킬 수 있음을 확인하였다.