1. 서 론

복잡한 문제에 대한 컴퓨터 시뮬레이션은 막대한 계산시간을 요구한다. 최근에는 이러한 계산시간의 부담을 줄이기 위해 시뮬레이션 결과를 데이터화 하여 대리모델(surrogate model)을 구성하는 방법이 널리 쓰이고 있다. 여러 대리모델 중 크리깅 모델(KM: Kriging Model)은 비교적 적은 데이터를 필요로하기 때문에 가장 많이 사용되고 있다. 특히, 크리깅 모델은 생성된 대리모델의 불확실성의 정량화(uncertainty quantification)가 가능하여 대리모델을 개선하기 위한 추가적인 데이터를 구할 수 있기 때문에 대리모델을 지속적으로 개선할 수 있는 장점이 있다. 이러한 크리깅 모델은 사용하는 기저함수와 데이터 사이의 관계를 나타내는 상관 함수(correlation function)에 따라 그 성능이 달라진다.

일반적으로 크리깅 모델의 기저함수로 상수(ordinary Kriging), 1차 또는 2차(universal Kriging) 다항함수를 많이 사용한다. 크리깅 모델에서는 고차의 기저함수를 사용하더라도 고정된 기저함수를 사용하면 국부적으로 비선형성이 큰 문제에 대한 근사화는 실패할 수 있다(Lee and Choi, 2011; Zhao et al., 2011). Zhao 등(2011)은 이러한 문제를 해결하기 위해 샘플링 데이터에 따라 최적의 기저함수를 선택할 수 있는 동적 크리깅 방법(DKM: Dynamic Kriging Method)를 개발하였다. 이때, 최적의 기저함수를 구하기 위해 프로세스 분산(process variance)을 적합함수(fitness function)로 한 유전자 알고리즘(GA: Genetic Algorithm)을 사용하였다. 이때, 데이터 사이의 상관관계를 나타내는 하이퍼 매개변수(Hyper-parameters)는 최대 우도 함수 평가(MLE: Maximum Likelihood Estimation)를 통해 구하게 된다. 빠르고 정확한 MLE를 위해서 일반화된 패턴 서치(GPS: Generalized Pattern Search) 방법을 사용하였다.

GA과정에서 프로세스 분산을 적합함수로 이용하는 경우 고정된 하이퍼 매개변수를 사용하면 최적의 기저함수를 찾는 것에 실패할 수 있다. Liang 등(2014)은 GA과정에서 하이퍼 매개변수를 고정할 경우 프로세스 분산의 값은 항상 줄어드는 것을 증명하고, 적합 함수로 프로세스 분산 대신 교차 검증 오차(CVE: Cross Validation Error)를 선택하여 개선된 크리깅 모델을 제시하였다. 하지만, 이 방법은 최적의 기저함수를 찾기 위해 각 기저함수마다 하이퍼 매개변수를 찾기 위한 GPS를 수행하여야 하고, GA의 자체의 계산비용이 막대하기 때문에 매우 비효율적이다. 뿐만 아니라 샘플수와 문제의 차원이 늘어남에 따라 최대 기저함수의 차수가 과도하게 증가하게 되는 단점이 있다.

Kang 등(2019)는 크리깅 모델에서 최적의 기저함수 조합을 구할 때 GA를 사용하는 대신 개별 기저함수의 CVE를 구하고 중요도를 평가하는 기저 스크리닝 기반 크리깅 모델(BSKM: Basis Screening based Kriging Model)을 제안하였다. BSKM은 기저함수의 최대 차수 제한하고 크리깅의 모델의 CVE가 최소가 될 때까지 개별 기저함수의 중요도가 높은 순으로 기저함수를 하나씩 추가하며 최적의 기저함수 조합을 찾는다. 이 과정에서 크리깅 모델은 반복적으로 생성해야 하며, 동시에 데이터 사이의 상관관계를 나타내는 하이퍼 매개변수도 최대 우도 평가방법을 통해 계산하여야 한다. Song 등(2013)는 MLE에 페널티를 적용한 최대 우도 평가 방법(PMLE : Penalized MLE)을 사용하여 샘플수가 적고, 샘플 사이의 공간적인 거리보다 하이퍼 매개변수의 크기가 작은 문제에 대해서 하이퍼 매개변수를 정확하게 구하는 방법을 제시하였다. 하지만, 이 방법은 최적의 페널티 값을 구하기 위해 페널티 값을 그리드(grid)로 나누어 반복적으로 MLE를 계산해야 하기 때문에 계산 비용에 대한 부담을 가지고 있다.

BSKM에서는 STEP 1) 다항함수의 최대 차수제한, STEP 2) 각 기저함수의 중요도 평가, STEP 3) CVE를 활용한 기저함수의 결정과 같은 순차적 과정을 거쳐 최적 기저함수를 정한다. 이러한 순차적 과정에서 하이퍼 매개변수 값을 매번 계산해야 하며, 이 값에 따라 선택되는 최종 기저함수 조합이 달라지기 때문에 정확한 하이퍼 매개변수를 구하는 것은 크리깅 모델의 정확도에 막대한 영향을 미치게 된다. 본 논문에서는 BSKM에 PMLE(Li and Sudjianto, 2005)을 적용하여 생성된 크리깅 모델의 정확도를 높였다. 계산 비용의 효율성을 높이기 위해 고정된 페널티 값을 사용하였고, 몇몇의 수학 모델에 제시된 방법을 적용하여 BSKM 의 정확성이 개선될 수 있음을 확인하였다.

2. 본 론

이 장에서는 BSKM을 소개한 후, 하이퍼 매개변수를 구하기 위한 MLE와 PMLE에 대한 수식 전개와 함께 이를 BSKM에 적용하는 과정을 나타내었다.

2.1 기저 스크리닝 기반 크리깅 모델(BSKM)

m차원을 갖는 임의의 샘플 값 x∈Rm에 대한 거동 함수(performance function)는 다음 식 (1)과 같다.

f(x)Tβ은 전역응답함수를 타나내고, f(x)은 사용자 정의의 기저함수 벡터로 K개의 기저함수로 이루어진 기저함수 벡터는 f(x)=[f1(x),f1(x),...,fK(x)]T로 나타낸다. Z(x)은 전역응답함수와 측정 데이터 사이의 오차로 분산 σ2에 대해 가우시안 분포 N(0,σ2)을 따르며, 두 데이터 다음과 xi와 xj에 대해 cov[Z(xi),Z(xj)]=R(θ,xi,xj)와 같은 상관관계를 갖는다고 가정한다. 상관함수는 다음과 같다.

여기서, 하이퍼 매개변수는 θ=[θ1,θ2,...,θm]T이며, xi,l는 샘플 xi의 l번째 요소를 나타낸다. 총 n개의 샘플 xi에서의 거동값 yi=Y(xi)로 이루어진 벡터를 관찰 벡터(observation vector)라 하고 y=[y1,y1,...,yn]T로 표현한다고 하자. 크리깅 모델은 모든 주어진 샘플을 지나면서 가중함수 w(x)와 y의 선형결합 Y^(x)=w(x)Ty로 표현할 수 있다. 거동 함수 Y(x)와 크리깅 모델 Y^(x) 평균제곱 오차가 최소가 되도록 가중함수값 w(x)을 찾으면, 다음 식 (3), (4)와 같이 최종적인 크리깅 모델식을 얻을 수 있다.

행렬 R은 (i,j)-성분이 Rij=R(θ,xi,xj)인 대칭 상관관계 행렬을 나타낸다. n개의 샘플 xi(i=1,2,...,n)에 대해 n×K 크기의 기저함수 행렬 F과 크기 n의 상관 함수 벡터 r(x)는 각각 다음 식 (5), (6)과 같이 표현한다.

사용자 정의의 기저함수 f(x)를 정할 때 대부분의 크리깅 모델은 다항함수를 이용하며, Pmax차 다항함수는 다음과 같다.

여기서, 최대차수 Pmax는 다음 식과 같이 주어진 샘플수 n과 차원 m값에 의해 결정되게 된다.

기존의 동적 크리깅 방법에서는 식 (8)에 의해 샘플의 수와 문제의 차원이 증가할 때 기저함수의 다항식 최대 차수가 과도하게 높아지는 경향이 있을 수 있다. Kang 등(2019) 크리깅 모델 구성시 최적의 기저함수 조합을 구할 때 개별 기저함수의 CVE를 구하고 중요도를 평가하여 최대 차수를 제한하고 최적의 기저함수 조합을 선택하는 기저 스크리닝 기반 크리깅 모델(BSKM: Basis Screening based Kriging Model)을 제안하였다. BSKM에서 최적의 기저함수는 다음과 같은 과정을 통해서 결정할 수 있다.

(STEP 1) 다항함수의 최대 차수 제한

다항식의 최대 차수는 다음 식 (9)에 의해 결정한다.

여기서, RSMEXY는 크리깅 모델의 교차 검증 평균 제곱근 오류(cross-validation root-means-square error)로 k-fold 교차검증에 대해서 다음 식 (10)과 같이 계산할 수 있다.

eXY(j)(xi)는 j번째 샘플의 부분집합에 대한 교차검증 오차이며, Y-j^(xi)가 j번째 샘플의 부분집합을 제외하고 생성한 크리깅 모델이라고 할 때, eXY(j)(xi)=Y(xi)-Y-j^(xi)와 같이 계산한다. 식 (7)의 다항식의 요소를 0차부터 Pmax차까지 하나씩 대입하면서 RSMEXY값을 구하고, RSMEXY값이 최소가 되는 Popt값을 정한다. 이 과정에서 총 Pmax+1개의 크리깅 모델을 생성해야 한다.

(STEP 2) 각 기저함수의 중요도 평가

(STEP 1)에서 결정한 Popt차 다항함수의 각 기저함수의 중요도를 평가한다. 각 기저함수에 대한 크리깅 모델의 평균제곱 k-foldCVE를 이용하며 그 기저함수의 중요도를 다음 식 (11)을 이용하여 평가한다.

e-α(j)(xi)는 𝛼번째 기저함수를 제외 했을 때의 j번째 fold에 대한 CVE를 나타내며, e-α(j)(xi)=Y(xi)-Y^-j,-α(xi)로 계산된다. Y^-j,-α(xi)은 𝛼번째 기저함수와 j번째 fold 샘플을 제외하고 생성한 크리깅 모델이며, Kopt는 Popt차 다항함수의 전체 집합의 요소수이다. 여기서, E-α의 값이 크다는 것은 𝛼번째 기저함수를 제외하면, CVE가 늘어난다는 뜻으로 그만큼 𝛼번째 기저함수의 중요도가 크다는 의미이다. 이번 과정에서는 앞선 과정에서 중복된 것을 제외하면, 총 Kopt-1번의 크리깅 모델을 생성하게 된다.

(STEP 3) CVE를 활용한 기저함수 조합 결정

Popt차 다항함수의 전체 집합 내에서 각 기저함수의 중요도 E-α를 평가한 후 개별 기저함수를 중요도 순으로 추가하면서 k-fold CVE가 최소가 되는 기저함수의 조합을 찾는다. 이때의 기저함수의 조합이 최적의 기저함수 조합이 된다. 이번 과정에서는 CVE 계산을 Popt차 다항함수의 전체 집합의 수만큼 계산하게 되므로 이전 과정과 마찬가지로 Kopt-1의 크리깅 모델을 생성하게 된다. BSKM은 비록 Pmax+2Kopt-1번의 크리깅 모델을 생성하지만, 기존의 GA 기반의 동적 크리깅 방법에 비해서는 크리깅 모델 생성 횟수가 매우 적기 때문에 매우 효율적으로 모델을 생성할 수 있는 장점이 있다. Kang 등(2019)은 BSKM을 Liang 등(2014)이 개발한 GA기반의 동적 크리깅 방법(DK-CVE)과 비교하여 계산 효율성과 정확성을 검증하였다.

2.2 최대 우도 평가 방법(MLE)

크리깅 모델은 식 (2)와 같이 주어진 샘플 사이의 상관관계를 이용하여 모델을 생성한다. 상관관계를 나타내는 하이퍼 매개변수 θ=[θ1,θ2,...,θm]T는 샘플 값 y에 대한 다음의 우도함수가 최대가 되도록 한다.

지수함수 식 (12)에 로그를 취해 대수 함수로 바꾸어 최대 우도 함수를 만족시키는 하이퍼 매개변수를 구하는 식은 다음과 같다.

식 (13)은 원점 근처에서 비선형성이 크며, 그 외의 지역에서는 매우 넓은 영역에 걸쳐 국부 최적점을 갖는 평평한 모양의 함수이기 때문에 하이퍼 매개변수에 대한 최적점을 찾는 것은 매우 어렵다. Zhao 등(2011)은 식 (13)의 해를 구하기 위해 일반화된 패턴 서치(GPS)방법을 사용하였으며, 이 방법이 최적 하이퍼 매개변수를 찾기 위해 많이 사용되는 수정된 후크-지브스(H-J: modified Hooke and Jeeves)방법과 레븐버그-마쿼드(L-M: Levenberg and Marquardt)방법보다 최대 우도함수 문제를 정확하고 효율적으로 풀 수 있다는 것을 보였다.

2.3 페널티를 적용한 최대 우도 평가 방법(PMLE)

식 (13)에 GPS 방법을 사용하더라도 여전히 국부 최적점이 존재하기 때문에 하이퍼 매개변수의 초기값을 어떻게 설정하느냐에 따라 최적점이 다르게 구해지는 문제가 있다. BSKM과 같이 각 기저함수별로 KM을 구해가면서, 순차적 최적 기저함수를 구하는 문제에서 하이퍼 매개변수의 초기값이 적절하지 않을 경우 각 단계별 오차의 누적으로 KM 모델이 정확하게 생성되지 않을 수 있다.

본 논문에서는 하이퍼 매개변수의 초기값 영향을 줄이고, 최대 우도 함수 평가에서 국부 최적점을 회피하기 위해 Li와 Sudjianto(2005)가 제안한 페널티를 적용한 최대 우도 평가 방법(PMLE : Penalized MLE)를 활용하고자 한다. PMLE는 샘플수가 적고, 샘플 사이의 공간적인 거리보다 하이퍼 매개변수의 크기가 작을 경우 MLE를 통한 하이퍼 매개변수 값의 정확성을 개선한다. PMLE를 이용한 최적의 하이퍼 매개변수를 구하는 최적화 식은 다음과 같이 변형하여 나타낼 수 있다.

여기서, pλ(|θ|)은 페널티 함수로 다양한 형태의 함수를 사용할 수 있다. 아래 식 (15)와 (16)의 경우 L1 또는 L2 형태 함수로 페널티 값 𝜆이 일정할 때 𝜃 값이 ‘0’의 값에서 멀어질수록 계속 증가하는 형태를 가진다.

이와 다르게 ‘0’의 값에서 일정 구간까지 증가하다 일정해지는 형태인 Smoothly Clipped Absolute Deviation(SCAD) 페널티 함수도 사용할 수 있다(Chu et al., 2011). Li와 Sudjianto (2005)는 하이퍼 매개변수𝜃에 대한 MLE의 1차와 2차 설계 민감도를 계산하고 뉴턴-랩슨(Newton-Raphson)방법과 피셔 채점 알고리즘(Fisher Scoring Algorithm)과 같은 반복적인 파라미터 업데이트 방법을 이용하여 우도함수가 최대가 되도록 하는 하이퍼 매개변수 𝜃, 크리깅 모델의 전역값 f(x)Tβ^, 분산 σ2 그리고 페널티 값 𝜆을 구하였다. Song 등(2013) 페널티 값 𝜆를 몇 개의 그리드(grid)로 나누어 각 그리드 𝜆 값에 대해 반복적으로 GPS를 이용하여 MLE의 값이 최소가 되는 하아 매개변수 𝜃를 구하였다. 위의 두 방법 모두 하이퍼 매개변수와 페널티 값을 구하기 위해 반복적으로 MLE를 계산을 해야 하기 때문에 계산 비용에 대한 부담을 가지고 있다.

본 논문에서는 BSKM에서 초기 하이퍼 매개변수 𝜃에 대한 기저함수 선택 오차를 줄이기 위해 PMLE 방법을 BSKM에 적용하였다. PMLE 최소가 되는 하이퍼 매개변수 값 𝜃을 구하기 위해서 GPS를 사용하였으며, 계산 비용의 효율성을 높이기 위해 고정된 페널티 값 𝜆를 사용하였다. Branin-Hoo 모델을 통해 고정된 페널티 값을 사용하는 것이 반복적인 계산으로 페널티 값을 업데이트 하는 것에 비해 정확성이 크게 다르지 않음을 보이도록 하겠다.

2.4 수치예제 결과 및 고찰

2.4.1 수학 검증 모델

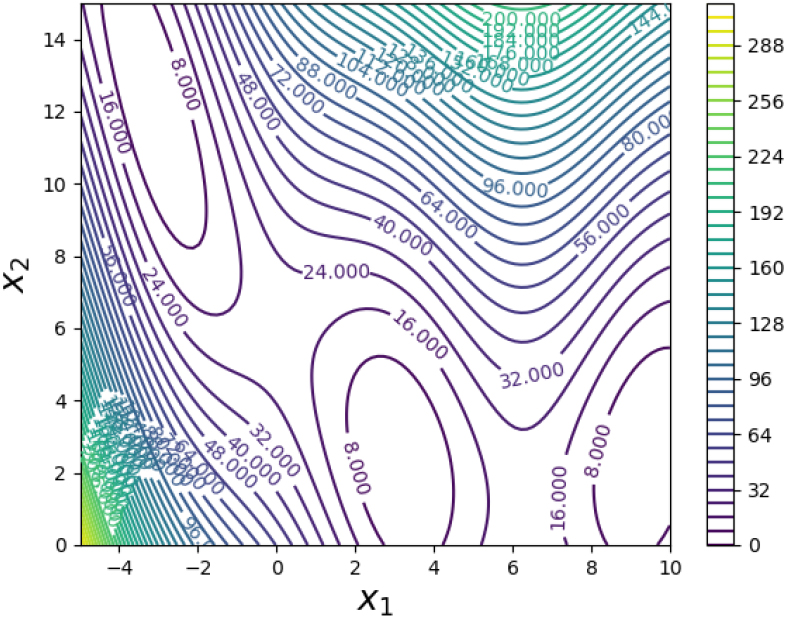
Kang 등(2019)는 2차원 문제에서부터 고차원의 비선형 문제에 대한 다양한 수학적 검증 모델을 활용하여 BSKM의 정확성과 효율성을 이미 검증하였다. 본 논문에서는 PMLE를 적용하여 BSKM의 정확성 개선 효과를 살펴보기 위해 Kang 등(2019)에서 제시한 수학적 모델 중 비선형성이 크며, 모델 생성에 비교적 적은 샘플수를 요구하는 Branin-Hoo 함수를 사용하였다(Liang et al., 2014). Branin-Hoo 함수식은 식 (17)과 같으며, 함수 모양은 Fig. 1과 같다.

프로그램 코딩에 python3을 이용하였으며, BSKM 모델 생성을 위해 총 18개의 샘플값을 이용하였다(Table 1).

Fig. 1.

Branin-Hoo function

2.4.2 PMLE 적용 BSKM

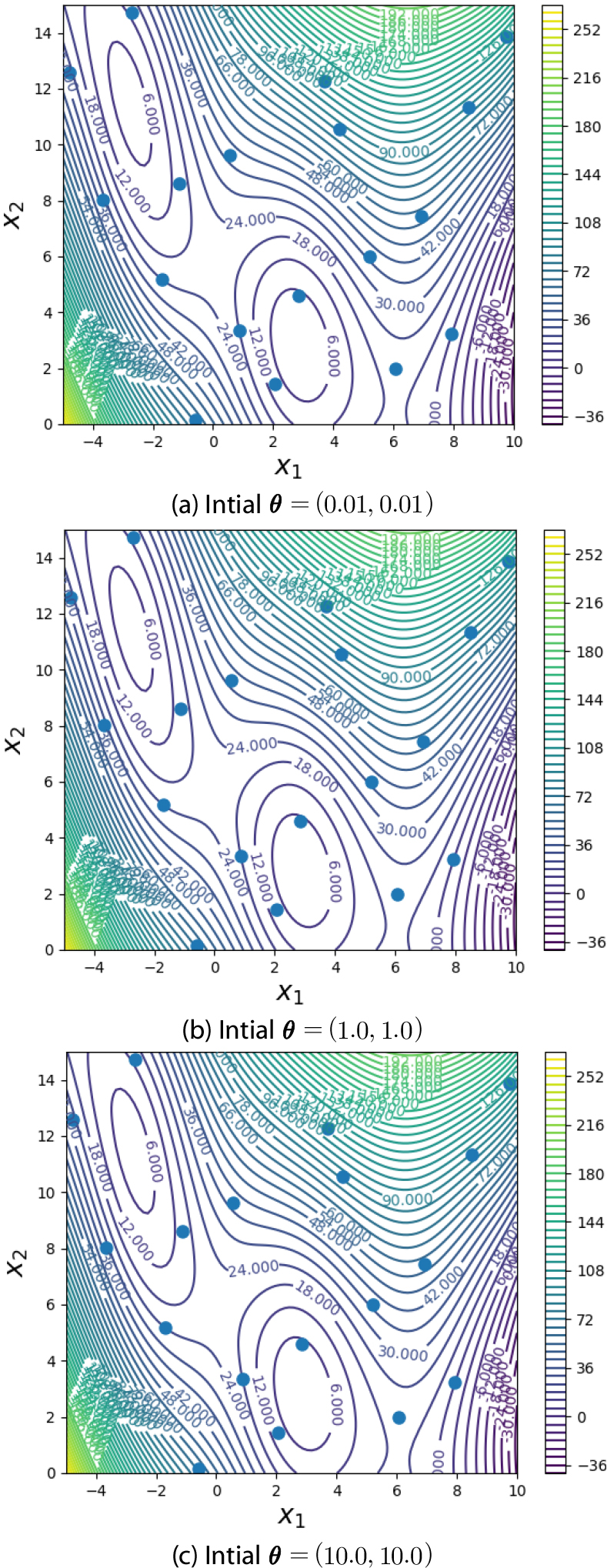
식 (13)의 로그로 표현된 우도함수(MLE)는 국부 최적점을 갖는 함수이기 때문에, GPS를 사용하더라도 하이퍼 매개변수 𝜃의 초기값에 따라 최적 하이퍼 매개변수의 값이 달라질 수 있다. 이러한 문제를 해결하기 위해서 식 (15)의 L1 페널티 함수에 대해 페널티 값은 𝜆=10.0을 사용한 PMLE를 BSKM에 적용해 보았다. 식 (14)의 최적화 문제를 풀 때 수치적인 안정성을 위해 0.001≤θi≤20.0(i=1,2,...,m)의 제한조건을 부여하였다. Table 2는 식 (17)로 주어진 Branin-Hoo 함수에 MLE와 PMLE를 BSKM에 각각 적용했을 때 하이퍼 매개변수의 초기값에 따른 최적 하이퍼 매개변수값 𝜃와 이때의 기저함수 그리고 평균 제곱근 오차(RMSE: Root Mean Square Error)값을 나타내고 있다.

BSKM에 MLE를 사용하였을 경우, 초기 𝜃값에 따라 최적 𝜃값이 달라지는 것을 알 수 있으며, Fig. 2의 결과와 같이 초기 𝜃값이 원점에서 멀어질수록 부정확한 결과를 얻을 수 있음을 알 수 있다. 이는 앞서 언급하였듯이, 𝜃값이 원점에서 멀어질수록 식 (13)으로 주어진 우도함수의 모양이 평평하여, 𝜃값이 변하더라도, 우도함수 값이 크게 변하지 않기 때문에 원점 근처에서 𝜃값의 최적점이 존재하는 경우 수치적으로 국부 최적점에 빠지기 쉽기 때문이다. 반면에 PMLE는 페널티 함수가 𝜃값이 원점에 가까운 값을 가질 수 있도록 강제하기 때문에 초기 하이퍼 매개변수의 값이 크더라도 원점 근처의 최적점 𝜃를 찾을 수 있도록 한다.

Fig. 2.

Branin-Hoo function (MLE)

Table 2에서 알 수 있듯이, PMLE를 BSKM에 적용했을 때 최적 𝜃값이 원점 근처에 존재하며, 이 경우 초기 𝜃값에 상관없이 최적점을 찾을 수 있음을 알 수 있다. Fig. 3은 PMLE를 적용했을 때 초기𝜃값에 따른 BSKM의 결과를 보여준다.

Fig. 3.

Branin-Hoo function (PMLE, 𝜆=10.0)

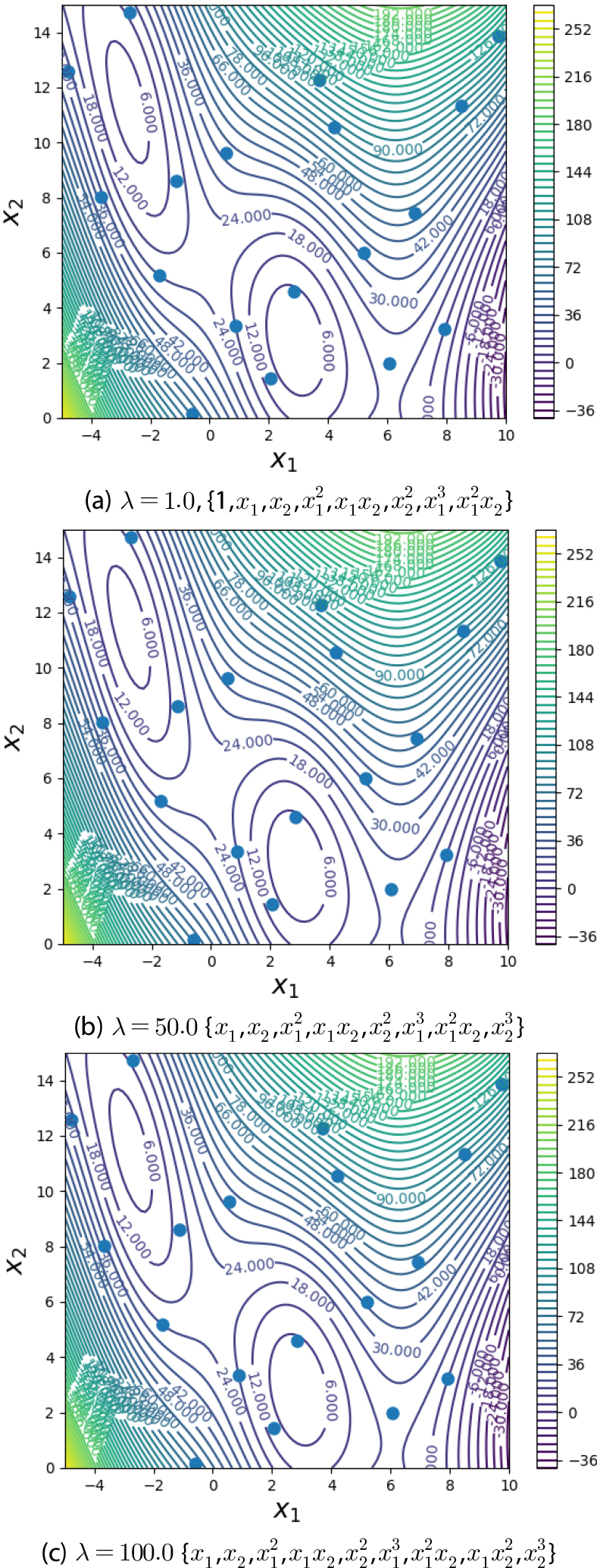
Table 3은 초기 하이퍼 매개변수가 𝜃=(1.0, 1.0)일 경우 페널티 값 𝜆에 대한 최적 𝜃값과 RMSE 값의 결과이다. 페널티를 적용하였을 때, 𝜆 값이 𝜆=1.0~10.0 범위일 경우 얻어진 최적 기저함수는 Table 2의 PMLE를 사용한 결과와 같이 {1,x1,x2,x12,x1x2,x22,x13,x12x2}이며, 𝜆 값이 변함에 따라 최적 𝜃값은 다소 변하나 RMSE의 변화는 거의 변화가 없다. 𝜆=50.0과 𝜆=100.0 같이 𝜆값이 과도하게 커질 경우 최적 𝜃값이 원점에 더 가까워지며, 이에 따라 기저함수는 각각 {x1,x2,x12,x1x2,x22,x13,x12x2,x23}와 {x1,x2,x12,x1x2,x22,x13,x12x2,x1,x22,x23}로 달라진다. 하지만, 모든 경우에 𝜆이 변하더라도 RMSE가 크게 변하지 않고, BSKM이 Fig. 1의 함수를 정확하게 재현하는 것을 Fig. 4에서 확인할 수 있다.

Fig. 4.

Branin-Hoo function (PMLE, 𝜃=(1.0, 1.0))

Table 4는 Li와 Sudjianto(2005)가 제안한 방법인 하이퍼 매개변수와 함께 페널티 값을 반복적으로 업데이트 하는 방법(fully iteration method)과 Song 등(2013)이 제안한 페널티 값 𝜆를 몇 개의 그리드(grid)로 나누어 BSKM의 CVE값이 최소가 되도록 하는 값 𝜆을 구하고 최적의 하이퍼 매개변수를 찾는 방법(grid based method), 그리고 본 논문에서 제안하는 고정된 페널티 값에 대한 PMLE방법에 대해 최적 하이퍼 매개변수 값과 계산시간을 비교한 결과를 보여준다.

각 방법에 대해서 초기 하이퍼 매개변수의 값은 𝜃=(1.0, 1.0)이다. 모든 방법은 Fig. 1의 함수를 매우 정확하게 재현하며, 기저함수는 {1,x1,x2,x12,x1x2,x22,x13,x12x2}로 Table 2의 PMLE의 결과와 같다. fully iteration method에서 구해진 페널티 값은 8.5294이며, grid based method에서 구해진 페널티 값은 페널티의 그리드를 20개와 50개로 나누었을 경우 모두 10.0으로 계산되었다. grid based method는 나누는 그리드의 개수에 따라 계산시간이 비례하여 증가하는 것을 알 수 있으며, 그리드를 20개로 나눈 경우 fully iteration method와 비슷한 계산시간이 요구되는 것을 알 수 있다. grid based method의 경우 최적 하이퍼 매개변수 값이 fully iteration method와 비슷하게 나오는 것을 확인할 수 있다. 본 논문에서 제시하는 방법에서 페널티 값은 grid based method에서 얻어진 값과 동일하나 최적 하이퍼 매개변수 값은 다소 차이가 나는 것을 알 수 있는데, 이는 BSKM 방법이 최적 기저함수가 기저함수 중요도에 따라 순차적으로 업데이트 되는 내역이 다르기 때문이다(history dependent property). 본 논문에서 제시하는 방법은 고정된 페널티 값을 사용하여 반복계산을 피하기 때문에 계산효율이 가장 높으며 더불어 KM의 정확성을 높이는 것을 알 수 있다.

3. 결 론

본 논문에서는 BSKM 생성의 정확도를 높이기 위해 페널티를 적용한 최대 우도 평가 방법을 제시하였다. 하이퍼 매개변수의 값에 따라 선택되는 최적의 기저함수 조합이 달라지기 때문에 정확한 MLE 계산은 크리깅 모델의 정확도에 막대한 영향을 미치게 된다. 정확한 하이퍼 매개변수를 계산하기 위해서 PMLE 방법을 적용하였으며, Branin-Hoo 함수 문제를 통해 BSKM의 정확성과 함께 고정된 페널티 값을 사용하여 계산 효율성을 동시에 개선하였다.