Seismic Fragility Analysis of Single-Degree-of-Freedom Model Based on Input Earthquake Ground Motions in Strong and Low-to-Moderate Seismic Regions

Sangki Park; Jeong-Rae Cho; Chang-Beck Cho; Dong-Chan Kim; Jinhyuk Lee

doi:10.7734/COSEIK.2023.36.6.371

Preview

Research Paper

Journal of the Computational Structural Engineering Institute of Korea. 31 December 2023. 371-380
https://doi.org/10.7734/COSEIK.2023.36.6.371

Seismic Fragility Analysis of Single-Degree-of-Freedom Model Based on Input Earthquake Ground Motions in Strong and Low-to-Moderate Seismic Regions

강진 및 중･약진 지역의 입력 지진파에 따른 단자유도 모델의 지진취약도 분석

Sangki Park¹

Jeong-Rae Cho²

Chang-Beck Cho¹

Dong-Chan Kim³

Jinhyuk Lee⁴^*

박 상기¹

조 정래²

조 창백¹

김 동찬³

이 진혁⁴^*

¹Senior Researcher, Department of Structural Engineering, Korea Institute of Civil Engineering and Building Technology, Goyang, 10223, Korea

²Senior Research Fellow, Department of Structural Engineering, Korea Institute of Civil Engineering and Building Technology, Goyang, 10223, Korea

³Postdoctoral Researcher, Department of Geotechnical Engineering, Korea Institute of Civil Engineering and Building Technology, Goyang, 10223, Korea

⁴Postdoctoral Researcher, Department of Structural Engineering, Korea Institute of Civil Engineering and Building Technology, Goyang, 10223, Korea

¹한국건설기술연구원 구조연구본부 수석연구원

²한국건설기술연구원 구조연구본부 선임연구위원

³한국건설기술연구원 지반연구본부 박사후연구원

⁴한국건설기술연구원 구조연구본부 박사후연구원

^{*Corresponding Author}

ABSTRACT

To calculate seismic fragility, it is important to select input earthquake ground motions that can properly express the characteristics of the target site. This study analyzed the seismic fragility of a single-degree-of-freedom (SDOF) model based on input earthquake ground motions in strong and low-to-moderate seismic regions. As a first step, a total of four sets of input earthquake ground motions were selected,: two sets measured near or far from overseas strong earthquake records and two sets exhibiting the characteristics of low-to-moderate earthquake regions in South Korea. A nonlinear SDOF model for three natural periods was applied to the target structure, and incremental dynamic analysis was used for fragility analysis. In addition, four damage states were defined, and seismic fragility results for each natural period of the nonlinear SDOF model for the four aforementioned input earthquake ground motion sets were obtained for each damage state.

Keywords

seismic fragility

input earthquake ground motions

natural period

damage state

incremental dynamic analysis

지진취약도를 산정하기 위해서는 목표 부지의 특성을 제대로 표현할 수 있는 입력 지진파의 산정이 중요하다. 본 논문에서는 국내외 강진 및 중‧약진 지역에서의 입력 지진파에 대한 단자유도 모델의 지진취약도를 분석하였다. 분석을 위한 첫 번째 단계로, 국외 강진 기록 중 근/원거리에서 측정한 2개의 입력 지진파 세트와 국내 중·약진 지역 특성에 적합한 입력 지진파 2개의 세트, 총 4개의 입력 지진파 세트를 선정하였다. 대상 구조물로는 3가지 고유주기에 대한 비선형 단자유도 모델을 적용하였고, 취약도 분석을 위해 증분동적해석을 이용하였다. 또한, 4가지 손상 상태를 정의하고, 손상 상태 각각에 대해 4가지 입력 지진파 세트의 고유주기별 지진취약도 결과를 제시하였다.

키워드

지진취약도

입력 지진파

고유주기

손상 상태

증분동적해석

MAIN

1. 서 론
2. 입력 지진파 세트 선정 및 단자유도 모델
2.1 입력 지진파 세트 선정
2.2 단자유도 모델
3. 지진취약도 함수
3.1 지진취약도 해석방법
3.2 손상 상태 정의
4. 지진취약도 분석
4.1 약간 손상(Slight, DS 1) 결과
4.2 보통 손상(Moderate, DS 2) 결과
4.3 심각 손상(Severe, DS 3) 결과
4.4 완전 손상(Complete, DS 4) 결과
5. 결 론

1. 서 론

지진취약도는 구조물의 특성과 지진 발생 환경을 고려하여 대상 구조물이 지진에 얼마나 취약한지를 확률적으로 평가하는 중요한 도구이다. 일반적으로 구조물의 손상 가능성을 평가하기 위해서는 지진의 강도(Intensity measure, IM)를 고려해야 하는데, 이때 대표적으로 사용되는 지진 강도 측정 지표로 최대지반가속도(Peak Ground Acceleration, PGA), 스펙트럼 가속도(Spectrum acceleration, Sa) 등이 있다(Baker, 2015; Choi et al., 2004; Kim and Song, 2010; Kong et al., 2022; Shinozuka et al., 2000). 지진취약도 산정을 위해서는 목표 부지의 특성을 제대로 표현할 수 있는 목표스펙트럼 또는 입력 지진파의 산정이 중요하다. 국내의 지진취약도 분석 연구의 경우, 해외 강진 기록, 한국형 인공지진 등의 입력 지진파를 활용한 지진취약도 산출과 관련된 연구는 최근까지도 다수 수행되었으나(Jeong et al., 2008; Kong et al., 2023; Lee et al., 2015, 2023; Park, et al., 2016), 국내 실정에 적합한 지진파를 활용하여 지진취약도를 분석하고, 적용 타당성을 검토하는 연구는 여전히 부족한 상황이다.

본 연구에서는 다양한 입력 지진파에 따른 지진취약도의 차이를 정량적으로 분석하고자 한다. 이를 위해 입력 지진파는 총 4개의 세트를 구성하였다. 먼저 기존 국외 강진 기록 중 근거리 측정, 원거리 측정 입력 지진파 세트인데, 각각 FEMA (2009), Somerville 등(1997)에서 제시한 총 2가지 지진파 세트를 활용하였다. 또한, 본 논문에서는 국내 중·약진 지역 특성에 적합하도록 입력 지진파를 산정한 연구에서 제시한 지진기록을 사용하였는데(Kim et al., 2016a, 2016b), 원데이터를 그대로 사용한 입력 지진파 세트와 국내 ‘내진설계기준(KDS 17 10 00)’의 설계응답스펙트럼을 반영한 입력 지진파 세트, 총 2가지를 사용하였다(MLIT, 2018).

2. 입력 지진파 세트 선정 및 단자유도 모델

2.1 입력 지진파 세트 선정

서론에서 언급한 바와 같이, Kim 등(2016a, 2016b)은 국내 지반조건에 부합하는 국내외 판내부 지진기록을 활용하여 중·약진 지진대인 한반도 특성에 적합한 설계응답스펙트럼을 제시하였다. 활용된 지진기록은 진앙거리 200km 이하의 18개 관측소에서 측정된 55개로, 국내 지진기록은 5개의 관측소에서 관측된 24개의 지진기록이며, 국외 지진기록은 13개 관측소에서 측정된 31개의 지진기록이다(Kim et al., 2016a, 2016b).

본 논문에서도 55개 지진기록을 별도의 가공없이 그대로 활용한 지진파 세트를 선정하였으며, 이를 ‘KDS17(Raw)’로 정의하였다. 또한, 우리나라 ‘내진설계기준(KDS 17 10 00)’에서 제시하고 있는 설계응답스펙트럼에 이들 55개의 지진기록을 매칭한 지진파 세트를 선정하고, 이는 ‘KDS17(Design)’으로 정의하였다. 본 논문에서 사용하고 있는 지진파는 평면상에 서로 직교하는 2개의 수평방향 지진파로 이루어져 x, y방향 55개씩, 총 110개의 지진파를 대상으로 하였으며, 진앙거리 범위는 1~199.2km, 규모의 범위는 4.8~7.9로 기록되었다.

해외 입력 지진파 세트를 구성하기 위해 FEMA(2009)에서 사용한 지진기록 중 22개의 원거리 지진파 세트를 사용하고, 이를 ‘FEMA695’로 정의하였다. 또한, Somerville 등(1997)은 SAC Steel Project를 통해 20개의 근거리 지진파 세트를 활용하였고, 본 논문에서도 이를 그대로 사용하였으며, ‘SAC’로 정의하였다. 근거리, 원거리 지진파 세트 또한 평면상에 서로 직교하는 2개의 수평방향 지진파로 이루어져 x, y방향 각각 22개, 20개씩, 총 44개, 40개의 지진파를 대상으로 하였다. 원거리 지진기록에 해당하는 ‘FEMA695’의 진앙거리 범위는 8.7~ 98.2km, 규모 범위는 6.5~7.6이고, 근거리 지진기록에 해당하는 ‘SAC’의 진앙거리 범위는 1.1~17.5km, 규모 범위는 6.7~7.4로 기록되었다. 즉, ‘FEMA695’와 ‘SAC’는 대부분의 강진 기록을 공유하지만, 진앙거리에서 원거리, 근거리 측정 여부에 대한 명확한 차이를 갖고 있다.

이처럼 본 연구에서도 지진취약도를 산출하기 위해 국내외 입력 지진파를 활용하였으며, Table 1, 2, 3과 같이 나타내었다.

Table 1

List of domestic earthquake and overseas intra-plate earthquake record set (Kim et al., 2016a, 2016b).

No.	Station Name	Nation	Earthquake name	Year	Magnitude	Epicentral Distance (km)	PGA (g)
1	HUK	South Korea	Hong island EQ	2003	4.90	85.44	0.011
2	MOP		Hong island EQ	2003	4.90	164.15	0.001
3	BUS		Offshore Uljin EQ	2004	5.20	199.20	0.001
4	CHJ					199.10	0.002
5	DAG					164.44	0.002
6	DGY					168.22	0.002
7	DGY		Odesan EQ	2007	4.80	7.52	0.156
8	BON					144.77	0.002
9	CEA					152.31	0.001
10	CHC					69.37	0.007
11	CHJ					105.43	0.002
12	CWO					104.51	0.005
13	ICN					112.72	0.002
14	MUS					162.69	0.008
15	PHA					180.14	0.001
16	SEO					149.48	0.002
17	SKC					68.39	0.003
18	SWO					149.31	0.003
19	TBA					70.07	0.008
20	WJU					56.75	0.028
21	GBI		Offshore Sinan EQ	2013	4.90	187.02	0.001
22	GBI		Seogyeongnyeolbi Island EQ	2014	5.10	101.48	0.007
23	DEI					147.00	0.008
24	BAR					116.29	0.005
25	ANL-768 Power Plant	America	Borah Peak, ID-01	1983	6.88	108.10	0.056
26	PBF					94.34	0.052
27	TRA-642 ETR Reactor Bldg.					86.15	0.030
28	CEM		Borah Peak, ID-02	1983	5.10	23.20	0.025
29	HAU		Borah Peak, ID-02	1983	5.10	50.43	0.033
30	Site 1		Nahanni, Canada	1985	6.76	6.80	1.100
31	Site 2					6.52	0.489
32	Site 3					22.36	0.148
33	Quebec		Saguenay, Canada	1988	5.90	154.92	0.051
34	Chicoutimi-Nord					37.77	0.131
35	St-Andre-du-Lac-St-Jean					62.31	0.156
36	Les Eboulements					93.99	0.125
37	Carlo		Denali, Alaska	2002	7.90	67.70	0.100
38	R109		Denali, Alaska	2002	7.90	61.85	0.109
39	CVVA		Mineral, Virginia	2011	5.80	53.80	0.122
40	GSH	Netherlands	Roermond, Netherlands	1992	5.30	57.67	0.012
41	OLF					82.71	0.006
42	WBS					103.49	0.009
43	Karakyr	Iran	Gazli, USSR	1976	6.80	12.82	0.718
44	Dayhook		Tabas, Iran	1978	7.35	20.63	0.406
45	Tabas		Tabas, Iran	1978	7.35	55.24	0.852
46	Abbar		Manjil, Iran	1990	7.37	40.43	0.515
47	BAM		Bam, Iran	2003	6.50	1.00	0.885
48	Chatrood		Zarand, Iran	2005	6.40	19.66	0.100
49	Bardsir					85.85	0.012
50	Sirch					94.24	0.013
51	Deh-Loulou					53.28	0.052
52	Qadrooni Dam					23.62	0.219
53	Shirinrood Dam					22.98	0.510
54	Davaran					61.38	0.056
55	KNI	India	Koynanagar, India	1967	6.50	10.80	0.490

Table 2

List of FEMA P-695, Far-Field record set (FEMA, 2009)

No.	Station Name	Nation	Earthquake Name	Year	Magnitude	Epicentral Distance (km)	PGA (g)
1	Capitola	America	Loma Prieta	1989	6.9	9.8	0.511
2	Gilroy Array #3		Loma Prieta	1989	6.9	31.4	0.559
3	Yermo Fire Station		Landers	1992	7.3	86	0.245
4	Coolwater		Landers	1992	7.3	82.1	0.417
5	Beverly Hills-Mulhol		Northridge	1994	6.7	13.3	0.488
6	Canyon Country-WLC		Northridge	1994	6.7	26.5	0.472
7	Hector		Hector Mine	1999	7.1	26.5	0.328
8	Delta		Imperial Valley	1979	6.5	33.7	0.35
9	El Centro Array #11		Imperial Valley	1979	6.5	29.4	0.379
10	El Centro Imp. Co.		Superstition Hills	1987	6.5	35.8	0.357
11	Poe Road (temp)		Superstition Hills	1987	6.5	11.2	0.475
12	Rio Dell IOverpass		Cape Mendocino	1992	7.0	22.7	0.549
13	LA-Hollywood Stor		San Fernando	1971	6.6	39.5	0.225
14	Bolu	Turkey	Duzce, Turkey	1999	7.1	41.3	0.806
15	Duzce		Kocaeli, Turkey	1999	7.5	98.2	0.364
16	Arcelik		Kocaeli, Turkey	1999	7.5	53.7	0.21
17	Nishi-Akashi	Japan	Kobe, Japan	1995	6.9	8.7	0.483
18	Shin-Osaka	Japan	Kobe, Japan	1995	6.9	46	0.233
19	Abbar	Iran	Manjil, Iran	1990	7.4	40.4	0.515
20	CHY101	Taiwan	Chi-Chi, Taiwan	1999	7.6	32	0.398
21	TCU045	Taiwan	Chi-Chi, Taiwan	1999	7.6	77.5	0.507
22	Tolmezzo	Italy	Friuli, Italy	1976	6.5	20.2	0.357

Table 3

List of SAC steel project, Near-Fault record set (Somerville et al., 1997)

No.	Station Name	Nation	Earthquake Name	Year	Magnitude	Epicentral Distance (km)	PGA (g)
1	Los Gatos	America	Loma Prieta, Los Gatos	1989	7.0	3.5	0.718
2	Lex. Dam		Loma Prieta, Lex. Dam	1989	7.0	6.3	0.686
3	Petrolia		C. Mendocino,Petrolia	1992	7.1	8.5	0.655
4	Lucerne		Landers	1992	7.3	1.1	0.799
5	Rinaldi		Northridge, Rinaldi	1994	6.7	7.5	0.89
6	Olive View		Northridge, Olive View	1994	6.7	6.4	0.732
7	Erzincan	Turkey	Erzincan	1992	6.7	2.0	0.457
8	Kobe JMA	Japan	Kobe	1995	6.9	3.4	1.088
9	Takatori	Japan	Kobe, Takatori	1995	6.9	4.3	0.786
10	Tabas	Iran	Tabas	1978	7.4	1.2	0.978
11	Simulated	Simulated	Elysian Park 1	-	7.1	17.5	0.892
12			Elysian Park 2			10.7	1.803
13			Elysian Park 3			11.2	1.013
14			Elysian Park 4			13.2	0.922
15			Elysian Park 5			13.7	1.162
16			Palos Vendes 1			1.5	0.974
17			Palos Vendes 2				0.968
18			Palos Vendes 3				0.873
19			Palos Vendes 4				0.793
20			Palos Vendes 5				0.916

2.2 단자유도 모델

Chopra와 Goel(2001)은 항복 변위 및 항복강도에 대해 단자유도(Single Degree of Freedom, SDOF) 시스템을 제시하였다. 모델의 고유주기(natural period, $T_{n}$ )는 0.5초, 자중(Weight, w)은 169.9kN, 높이(Height, h)는 3.66m, 항복강도 (yielding strength, $f_{y}$ )는 39.26kN, 항복 변위(yielding displacement, $d_{y}$ )는 0.01376m, 최대 변위(Maximum displacement, $d_{m}$ )는 0.07362m, 변형률 경화 계수(strain-hardening ratio, 𝛼)는 0.04이고, 연성계수(𝜇)는 5.35이다. Fig. 1에 단자유도 모델의 비선형 정적 해석 결과에 대한 이산화 곡선을 나타내었다. 본 연구에서도 Chopra와 Goel (2001)가 제안한 단자유도 모델을 활용하여 지진해석을 수행하였다. 또한, 응답스펙트럼 상 단주기 영역에 속하며 가속도 또는 속도에 민감하게 반응하는 고유주기인 0.15초, 변위에 민감하게 반응하는 고유주기 1.0초에 대한 단자유도 모델을 별도로 작성하였다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2023-036-06/N0040360603/images/Figure_jcoseik_36_06_03_F1.jpg

Fig. 1.

Push-over curve for bi-linear SDOF in natural period 0.5s

이때, 0.15초와 1.0초에 해당하는 단자유도 모델을 합리적으로 작성하기 위해 층간변위비(Drift ratio), 항복강도( $f_{y}$ ), 변형률 경화 계수(𝛼)는 고유주기 0.5초에 해당하는 값으로 고정하였다. 즉, 층간변위비(Drift ratio)는 항복 변위( $d_{y}$ )를 구조물의 높이(h)로 나눈 값인 0.00376, 항복강도( $f_{y}$ )는 39.26kN, 변형률 경화 계수(𝛼)는 0.04로 고정하였다. 이에 따라 대상 비선형 모델의 고유주기가 0.15초, 1.0초의 구조물의 높이(h)는 각각 1.168m, 7.32m로, 항복 변위( $d_{y}$ )는 각각 0.0044m, 0.0275m로 산출하였다. 고정된 층간변위비, 항복강도, 변형률 경화 계수를 제외한 고유주기별 단자유도 모델의 파라미터를 Table 4와 같이 정의하였다.

Table 4

Nonlinear SDOF parameters for three natural periods

Natural period (sec)	Weight (kN)	Height (m)	Yielding displacement (m)	Maximum displacement (m)	Stiffness (kN/m)
0.15	50.1	1.17	0.0044	0.0235	8,940
0.5	169.6	3.66	0.0138	0.0736	2,853
1.0	354.9	7.32	0.0275	0.1472	1,426

3. 지진취약도 함수

3.1 지진취약도 해석방법

지진취약도 함수는 지진의 강도에 따라 대상 구조물에 주어진 손상 상태에 대한 조건부 확률을 나타내는 것으로, 지진하중의 크기에 따라 주어진 조건에 대한 손상을 정량적으로 제시할 수 있다. 일반적으로 취약도 함수는 식 (1)과 같이 누적분포함수(cumulative distribution function) 함수로 나타낼 수 있다(Baker et al., 2021; Jeong et al., 2016; Lee et al., 2014; Shinozuka et al., 2000; Yi et al., 2021).

(1)

P [D S | I M = X] = Φ (\frac{\ln (X / θ)}{σ})

여기서, $P [D S | I M = X]$ 는 특정 손상 상태(Damage state, DS)에 대한 취약도 함수이며, $X$ 는 입력변수로, 지진의 강도를 나타내며, 본 연구에서는 최대지반가속도(PGA)를 사용하였다. $Φ (∙)$ 는 표준 정규분포 함수의 누적 확률 분포함수이며, 𝜃와 𝜎는 각각 중앙값(median)과 대수표준편차(lognormal standard deviation)이다.

지진취약도 곡선의 작도를 위해 필요한 중앙값(𝜃)과 표준편차(𝜎)가 필요하다. 중앙값(𝜃)과 표준편차(𝜎)의 값을 얻기 위해 다양한 분석 방법이 사용되고 있으며, 이 중에서 MSA (Multiple Strips Analysis), IDA(Incremental Dynamic Analysis), Cloud Analysis 등이 있다(Yi et al., 2021). 본 연구에서는 증분동적해석(IDA) 방법을 사용하였다(Vamvatsikos and Cornell , 2002, 2004). 구체적으로 지진 응답 등을 모사할 수 있는 Open Sees(Mazzoni et al., 2006)를 활용하여 4개의 입력 지진파 세트에 대하여 최대지반가속도를 기준으로 0.0~3.0g 범위에 대하여 증분동적해석(IDA)을 수행하였다.

3.2 손상 상태 정의

본 연구에서는 Table 5에서 나타낸 바와 같이 Barbat 등(2008)에서 제시한 4가지 손상 상태를 사용하였다. Table 5에서 확인할 수 있듯이 손상 상태를 기준으로 대상 구조물의 항복 변위( $d_{y}$ )와 최대 변위( $d_{m}$ )에 대한 식으로 구성된 것을 확인할 수 있다. 예를 들어 2.2절에서 소개한 고유주기 0.5초, 항복 변위( $d_{y}$ ) 0.01376m, 최대 변위( $d_{m}$ ) 0.07362m에 따른 대상 단자유도 구조물의 경우 약간 손상(Slight, DS1)에 해당하는 값은 0.00963m로 계산된다. 3가지 고유주기에 따른 손상 상태는 Table 6에 변위 값으로 계산하여 나타내었다.

Table 5

Definition of damage states (DS) level

Damage state (DS) level	Damage state	Threshold
DS 1	Slight	$0.7 * d_{y}$
DS 2	Moderate	$1.0 * d_{y}$
DS 3	Severe	$d_{y} + 0.25 (d_{m} - d_{y})$
DS 4	Complete	$1.0 * d_{m}$

Table 6

Damage Threshold displacement of damage states for three natural periods

Natural period (sec)	Threshold displacement of damage states (m)
Natural period (sec)	DS 1	DS 2	DS 3	DS 4
0.15	0.0031	0.0044	0.0092	0.0235
0.5	0.0096	0.0138	0.0287	0.0736
1.0	0.0193	0.0275	0.0575	0.1473

4. 지진취약도 분석

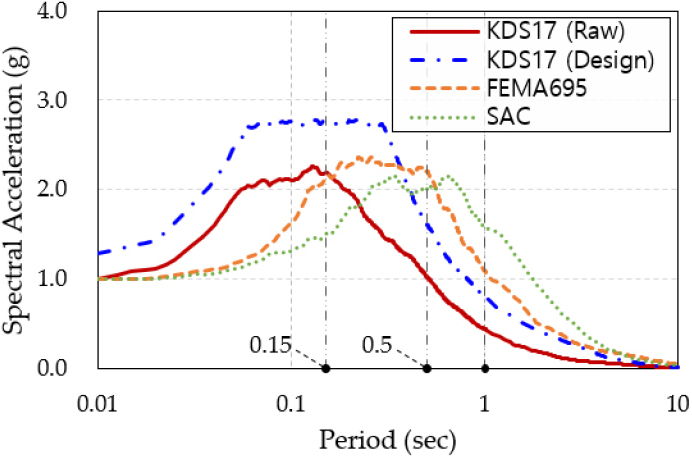
지진취약도 분석에 앞서 입력 지진파 세트에 대한 특성을 나타내기 위해 Fig. 2와 같이 4가지 입력 지진파 세트별 평균 가속도 응답스펙트럼 그래프를 작도하였다. 국내 지진파 세트에 따른 응답스펙트럼(‘KDS17(Raw)’, ‘KDS17(Design)’)은 0.15초 이하의 주기에서 가속도 응답이 최대가 되는 반면에 해외 지진파 세트에 따른 응답스펙트럼(‘FEMA695’, ‘SAC’)는 0.15초 이상의 주기에서 가속도 응답이 증폭되는 것을 관찰할 수 있다. 이를 통해 국내 지진파는 단주기 구조물에 해외 지진파는 장주기 구조물에 보다 큰 영향을 줄 것으로 예상할 수 있다. 또한, Table 7을 통해 세 가지 고유주기에 매칭되는 스펙트럼 가속도를 직관적으로 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2023-036-06/N0040360603/images/Figure_jcoseik_36_06_03_F2.jpg

Fig. 2.

Average acceleration response spectrum for four sets of input earthquake ground motions

Table 7

Spectral Acceleration of four sets for three natural periods

Natural period (sec)	Spectral Acceleration (g)
Natural period (sec)	KDS17 (Raw)	KDS17 (Design)	FEMA695	SAC
0.15	2.18	2.78	2.12	1.50
0.5	1.03	1.62	2.21	2.01
1.0	0.44	0.80	1.09	1.59

4.1 약간 손상(Slight, DS 1) 결과

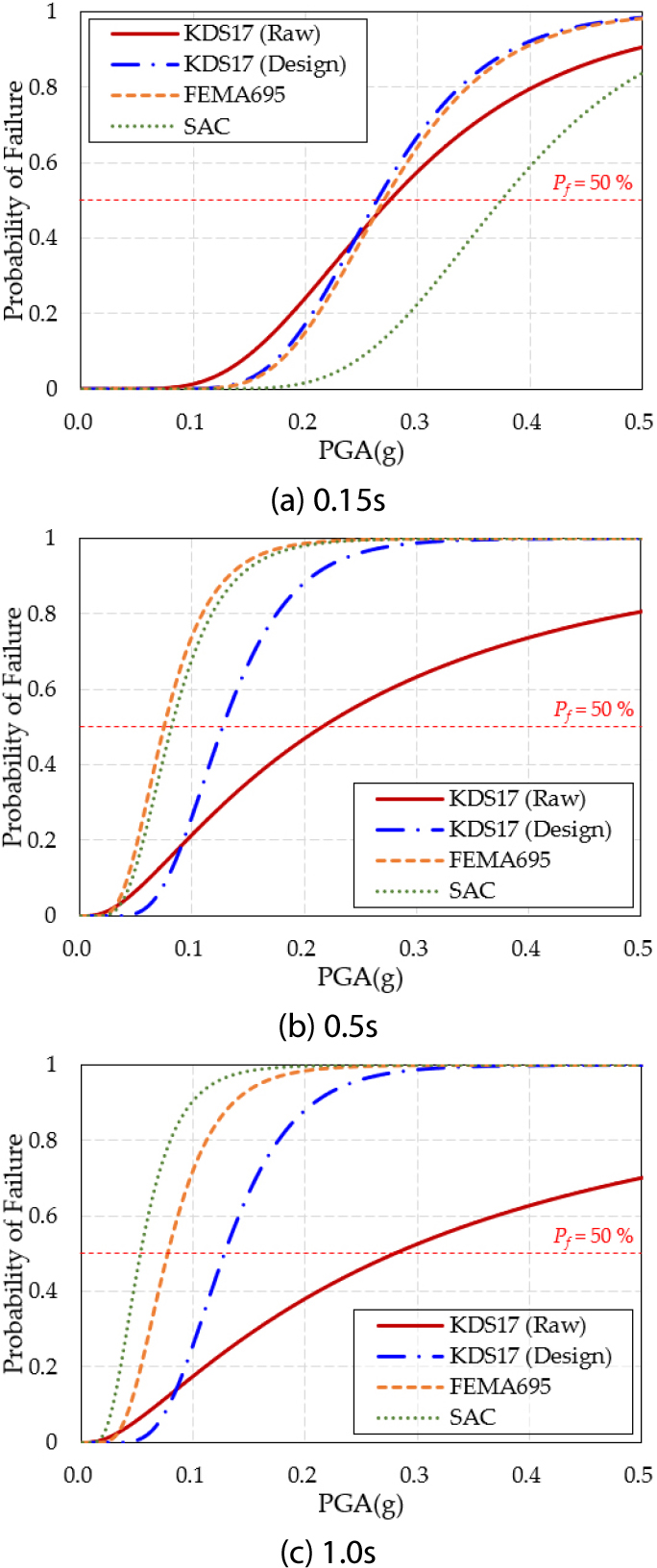
Fig. 3에 나타난 것과 같이 4가지 입력 지진파 세트를 활용하여 약간 손상(DS 1)에 대해 지진취약도 분석을 수행하였으며, Table 8, 9, 10은 고유주기에 따른 단자유도 구조물의 약간 손상(DS 1)에 대한 각 입력 지진파 세트의 지진취약도 변수를 나타내었다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2023-036-06/N0040360603/images/Figure_jcoseik_36_06_03_F3.jpg

Fig. 3.

Seismic Fragility curves at damage state level 1

Table 8

Seismic fragility parameters and results of damage state 1 (DS 1) in natural period 0.15s

Earthquake Set ID	Median (𝜃)	Standard deviation (𝜎)
KDS17 (Raw)	0.275	0.454
KDS17 (Design)	0.264	0.293
FEMA695	0.270	0.290
SAC	0.374	0.294

Table 9

Seismic fragility parameters and results of damage state 1 (DS 1) in natural period 0.5s

Earthquake Set ID	Median (𝜃)	Standard deviation (𝜎)
KDS17 (Raw)	0.215	0.972
KDS17 (Design)	0.127	0.381
FEMA695	0.075	0.445
SAC	0.082	0.435

Table 10

Seismic fragility parameters and results of damage state 1 (DS 1) in natural period 1.0s

Earthquake Set ID	Median (𝜃)	Standard deviation (𝜎)
KDS17 (Raw)	0.278	1.104
KDS17 (Design)	0.128	0.381
FEMA695	0.077	0.442
SAC	0.053	0.488

먼저, 구조물의 고유주기가 0.15초일 때 파괴 확률 50%를 기준으로 보면, ‘KDS17(Design)’, ‘FEMA695’, ‘KDS17(Raw)’, ‘SAC’의 순으로 취약한 것을 볼 수 있다. 이는 Table 8의 중앙값(𝜃)을 통해서도 확인할 수 있다. 즉, 중앙값(𝜃)은 파괴 확률 50%에서 x축 PGA에 해당하며, PGA값이 작을수록 취약하다. 고유주기가 0.5초인 경우, ‘FEMA695’, ‘SAC’, ‘KDS17(Design)’, ‘KDS17(Raw)’의 순으로 동일 파괴 확률 50%에 대해서 취약한 것을 볼 수 있고, 고유주기가 1.0초인 경우 ‘SAC’, ‘FEMA695’, ‘KDS17(Design)’, ‘KDS17(Raw)’ 순으로 취약한 것을 확인할 수 있다. 이때, 설계응답스펙트럼 매칭 등 별도의 가공없이 그대로 사용함에 따라 불확실성의 지표인 대수표준편차가 큰 ‘KDS17(Raw)’를 제외하고, 나머지 3개 입력 지진파 세트의 고유주기별 취약 우선순위에 집중하였다. 그 결과 단주기 영역에 해당하는 고유주기 0.15초의 경우, 파괴 확률 50% 기준에 대하여 ‘KDS17(Design)’이 가장 취약한 것을 알 수 있다. 반대로 중/장주기 영역에 해당하는 고유주기 0.5초, 1.0초의 경우, ‘FEMA695’, ‘SAC’ 순서로 가장 취약한 것을 확인하였다.

4.2 보통 손상(Moderate, DS 2) 결과

약간 손상(DS 1)의 분석 절차와 같이 Fig. 4를 보면, 4가지 입력 지진파 세트를 활용하여 보통 손상(DS 2)에 대해 지진취약도 분석을 수행하였으며, Table 11, 12, 13은 고유주기에 따른 단자유도 구조물의 보통 손상(DS 2)에 대한 각 입력 지진파 세트의 지진취약도 변수를 나타내었다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2023-036-06/N0040360603/images/Figure_jcoseik_36_06_03_F4.jpg

Fig. 4.

Seismic Fragility curves at damage state level 2

Table 11

Seismic fragility parameters and results of damage state 2 (DS 2) in natural period 0.15s

Earthquake Set ID	Median (𝜃)	Standard deviation (𝜎)
KDS17 (Raw)	0.391	0.454
KDS17 (Design)	0.374	0.251
FEMA695	0.383	0.285
SAC	0.533	0.291

Table 12

Seismic fragility parameters and results of damage state 2 (DS 2) in natural period 0.5s

Earthquake Set ID	Median (𝜃)	Standard deviation (𝜎)
KDS17 (Raw)	0.308	0.968
KDS17 (Design)	0.181	0.339
FEMA695	0.107	0.402
SAC	0.116	0.393

Table 13

Seismic fragility parameters and results of damage state 2 (DS 2) in natural period 1.0s

Earthquake Set ID	Median (𝜃)	Standard deviation (𝜎)
KDS17 (Raw)	0.400	1.106
KDS17 (Design)	0.182	0.338
FEMA695	0.110	0.399
SAC	0.074	0.446

구조물의 고유주기가 0.15초일 때, 파괴 확률 50%를 기준으로 보면 약간 손상(DS 1)의 결과와 마찬가지로 ‘KDS17(Design)’, ‘FEMA695’, ‘KDS17(Raw)’, ‘SAC’의 순으로 취약한 것을 볼 수 있다. 이는 Table 11의 중앙값(𝜃)을 통해서도 확인할 수 있다. 고유주기가 0.5초인 경우, ‘FEMA695’, ‘SAC’, ‘KDS17(Design)’, ‘KDS17(Raw)’의 순으로 동일 파괴 확률 50%에 대해서 취약한 것을 볼 수 있고, 고유주기가 1.0초인 경우 ‘SAC’, ‘FEMA695’, ‘KDS17(Design)’, ‘KDS17(Raw)’ 순으로 취약한 것을 확인할 수 있다. 이때, ‘KDS17(Raw)’를 제외하고 나머지 3개 입력 지진파 세트의 고유주기별 취약 우선순위를 살펴보면 단주기 영역에 해당하는 고유주기 0.15초의 경우, 파괴 확률 50% 기준에 대하여 ‘KDS17(Design)’이 가장 취약한 것을 알 수 있다. 반대로 중/장주기 영역에 해당하는 고유주기 0.5초, 1.0초의 경우, 각각 ‘FEMA695’, ‘SAC’ 순서로 가장 취약한 것을 확인하였다.

4.3 심각 손상(Severe, DS 3) 결과

보통 손상(DS 2)의 분석 절차와 같이 Fig. 5를 보면, 4가지 입력 지진파 세트를 활용하여 심각 손상(DS 3)에 대해 지진취약도 분석을 수행하였으며, Table 14, 15, 16은 고유주기에 따른 단자유도 구조물의 심각 손상(DS 3)에 대한 각 입력 지진파 세트의 지진취약도 변수를 나타내었다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2023-036-06/N0040360603/images/Figure_jcoseik_36_06_03_F5.jpg

Fig. 5.

Seismic Fragility curves at damage state level 3

Table 14

Seismic fragility parameters and results of damage state 3 (DS 3) in natural period 0.15s

Earthquake Set ID	Median (𝜃)	Standard deviation (𝜎)
KDS17 (Raw)	0.831	0.424
KDS17 (Design)	0.710	0.174
FEMA695	0.671	0.210
SAC	0.771	0.164

Table 15

Seismic fragility parameters and results of damage state 3 (DS 3) in natural period 0.5s

Earthquake Set ID	Median (𝜃)	Standard deviation (𝜎)
KDS17 (Raw)	0.683	0.917
KDS17 (Design)	0.396	0.244
FEMA695	0.245	0.302
SAC	0.226	0.321

Table 16

Seismic fragility parameters and results of damage state 3 (DS 3) in natural period 1.0s

Earthquake Set ID	Median (𝜃)	Standard deviation (𝜎)
KDS17 (Raw)	0.913	1.054
KDS17 (Design)	0.407	0.294
FEMA695	0.236	0.399
SAC	0.153	0.432

구조물의 고유주기가 0.15초일 때 파괴 확률 50%를 기준으로 보면, 약간 손상(DS 1), 보통 손상(DS 2)의 결과와는 달리 ‘FEMA695’, ‘KDS17(Design)’, ‘SAC’, ‘KDS17(Raw)’의 순으로 취약한 것을 볼 수 있다. 이는 Table 14의 중앙값(𝜃)을 통해서도 확인할 수 있다. 고유주기가 0.5초, 1.0초인 경우 ‘SAC’, ‘FEMA695’, ‘KDS17(Design)’, ‘KDS17(Raw)’의 순으로 동일 파괴 확률 50%에 대해서 취약한 것을 확인할 수 있다. 이때, ‘KDS17(Raw)’를 제외하고 나머지 3개 입력 지진파 세트의 고유주기별 취약 우선순위를 살펴보면 단주기 영역에 해당하는 고유주기 0.15초의 경우 파괴 확률 50% 기준에 대하여 ‘FEMA 695’가 가장 취약한 것을 알 수 있다. 중/장주기 영역에 해당하는 고유주기 0.5초, 1.0초의 경우 ‘SAC’가 가장 취약한 것으로 분석되었다.

4.4 완전 손상(Complete, DS 4) 결과

심각 손상(DS 3)의 분석 절차와 같이, Fig. 6을 보면, 4가지 입력 지진파 세트를 활용하여 완전 손상(DS 4)에 대해 지진취약도 분석을 수행하였으며, Table 17, 18, 19는 고유주기에 따른 단자유도 구조물의 완전 손상(DS 4)에 대한 각 입력 지진파 세트의 지진취약도 변수를 나타내었다.

https://cdn.apub.kr/journalsite/sites/jcoseik/2023-036-06/N0040360603/images/Figure_jcoseik_36_06_03_F6.jpg

Fig. 6.

Seismic Fragility curves at damage state level 4

Table 17

Seismic fragility parameters and results of damage state 4 (DS 4) in natural period 0.15s

Earthquake Set ID	Median (𝜃)	Standard deviation (𝜎)
KDS17 (Raw)	1.653	0.468
KDS17 (Design)	1.349	0.139
FEMA695	1.059	0.126
SAC	1.057	0.158

Table 18

Seismic fragility parameters and results of damage state 4 (DS 4) in natural period 0.5s

Earthquake Set ID	Median (𝜃)	Standard deviation (𝜎)
KDS17 (Raw)	1.612	0.869
KDS17 (Design)	0.913	0.260
FEMA695	0.563	0.303
SAC	0.407	0.379

Table 19

Seismic fragility parameters and results of damage state 4 (DS 4) in natural period 1.0s

Earthquake Set ID	Median (𝜃)	Standard deviation (𝜎)
KDS17 (Raw)	2.121	0.970
KDS17 (Design)	0.934	0.298
FEMA695	0.566	0.433
SAC	0.346	0.511

3가지 고유주기에 대하여 파괴 확률 50%를 기준으로 보면, ‘SAC’, ‘FEMA695’, ‘KDS17(Design)’, ‘KDS17(Raw)’의 순으로 취약한 것을 볼 수 있다. 또한, 심각 손상(DS 3) 취약도 결과에서 나타난 경향과 마찬가지로 ‘KDS17(Raw)’를 제외한 3가지 입력 지진파 세트의 지진취약도는 본 연구에서 적용된 단자유도 구조물의 특성과 세 가지 고유주기에 매칭되는 스펙트럼 가속도(Table 7)에 따라 나타난 경향으로 단주기 영역(0.15초)보다는 장주기 영역(0.5초, 1.0초)에서 더 취약한 것으로 분석되었다.

5. 결 론

본 연구에서는 국내외 지진기록을 통해 선별한 4가지 입력 지진파 세트와 단자유도 모델의 3가지 고유주기에 대한 지진취약도를 분석하였다. 입력 지진파는 해외 강진을 기반으로 산정한 원거리, 근거리에 따른 각각의 입력 지진파 2세트와 중·약진 지역 특성에 맞는 입력 지진파 2세트를 선정하였고, 고유주기별 대상 구조물 및 손상 상태에 대한 정의를 통해서 지진취약도 분석을 수행하였다.

4가지 손상 상태에 따른 3가지 고유주기별 지진취약도 분석 결과에서 ‘KDS17(Raw)’의 지진취약도가 ‘KDS17(Design)’, ‘FEMA695’, ‘SAC’의 지진취약도 대비 대수표준편차(𝜎)가 크고 완만한 곡선 개형을 보이는데, 다시 말해 이는 나머지 3가지 지진파 세트와 비교하여 ‘KDS17(Raw)’가 불확실성이 크다는 것을 의미한다. 이에 따라 ‘KDS17(Raw)’의 경우, 추후 본 논문에서 사용한 55개 지진기록에 대한 세분화, 지진 데이터의 무작위성(불확실성) 고려 등 후속 연구가 필요할 것으로 판단된다.

4가지 손상 상태에 대해서 대상 단자유도 구조물의 고유주기가 길어질수록(0.15→1.0초), 동일 파괴 확률 50%에 대한 취약 특성이 극명하게 나타나는 것으로 분석되었다. 특히, 해외 강진으로 구성된 ‘FEMA695’와 ‘SAC’의 취약도의 경우는 손상 상태가 심화될수록(DS 1→DS 4), 본 논문에서 제시한 단자유도 구조물의 특성과 입력 지진파 세트별 스펙트럼 가속도 경향에 따라 단주기(0.15초) 영역 대비 장주기 영역(0.5초, 1.0초)에서 더 취약한 것을 관찰할 수 있었다.

4가지 손상 상태별 장주기 고유주기에 해당하는(1.0초) 모든 지진취약도 결과를 보면 ‘SAC’, ‘FEMA695’, ‘KDS17(Design)’, ‘KDS17(Raw)’의 순으로 동일 파괴 확률 50%에 대해서 취약한 것으로 확인되었다. 이때, ‘SAC’는 해외 강진 기록 중에서도 근거리 입력 지진기록이 그대로 반영되어 손상 상태별 파괴 확률이 가장 큰 것으로 나타났다. 또한, 본 논문에서 제시한 단주기 구조물(0.15초)은 원거리 입력 지진파 세트(‘FEMA695’)에 취약하고, 장주기 구조물(1.0초)은 근거리 입력 지진파 세트(‘SAC’)에 취약한 것으로 분석되었다.

Acknowledgements

본 연구는 국토교통부/국토교통과학기술진흥원의 지원으로 수행되었음(과제번호 RS-2021-KA163162).

References

Baker J.W. (2015) Efficient Analytical Fragility Function Fitting Using Dynamic Structural Analysis, Earthq. Spectra, 31(1), pp.79~99. 10.1193/021113EQS025M

Baker J.W., Bradley, B.A., Stafford, P.J. (2021) Seismic Hazard and Risk Analysis, Cambridge University Press, pp.1~578. 10.1017/9781108425056

Choi, E., DesRoches, R., Nielson, B. (2004) Seismic Fragility of Typical Bridges in Moderate Seismic Zones, Eng. Struct., 26(2), pp.187~199. 10.1016/j.engstruct.2003.09.006

Chopra, A.K., Goel R.K. (2001) A Modal Pushover Analysis Procedure to Estimate Seismic Demands for Buildings: Theory and Preliminary Evaluation, PEER Report 2001/03, Pacific Earthquake Engineering Research Center, College of Engineering, University of California Berkeley, pp.5~7.

FEMA (2009) Quantification of Building Seismic Performance Factors (FEMA P695), Federal Emergency Managment Agency, Washington. D.C.

Jeong, G.H., Lee, H.S., Hwang, K.R., Kwon, O., Kim, S. (2016) Seismic Fragility Analysis of High-Rise RC Box-Type Wall Building Structures, J. Earthq. Eng. Soc. Korea, 20(3), pp. 155~162. 10.5000/EESK.2016.20.3.155

Jeong, S., Choi, S., Kim, K. (2008) Rapid Seismic Vulnerability Assessment Method for Generic Structures, J. Korea Concr. Inst., 20(1), pp.51~58. 10.4334/JKCI.2008.20.1.051

Kim, H.S., Song, J.K. (2010) Effect of Near- and Far-Fault Earthquakes for Seismic Fragility Curves of PSC Box Girder Bridges, J. Earthq. Eng. Soc. Korea, 14(5), pp.53~64. 10.5000/EESK.2010.14.5.053

Kim, J.K., Kim, J.H., Lee, J.H., Heo, T.M. (2016a) Development of Korean Standard Horizontal Design Spectrum Based on the Domestic and Overseas Intra-plate Earthquake Records, J. Earthq. Eng. Soc. Korea, 20(6), pp.369~378. 10.5000/EESK.2016.20.6.369

Kim, J.K., Kim, J.H., Lee, J.H., Heo, T.M. (2016b) Development of Korean Standard Vertical Design Spectrum Based on the Domestic and Overseas Intra-plate Earthquake Records, J. Earthq. Eng. Soc. Korea, 20(6), pp.413~424. 10.5000/EESK.2016.20.6.413

Kong, S., Kim, Y., Moon, J., Song, J. (2023) Development of System-Level Seismic Fragility Methodology for Probabilistic Seismic Performance Evaluation of Steel Composite Box Girder Bridges, J. Comput. Struct. Eng. Inst. Korea, 36(3), pp.173~184. 10.7734/COSEIK.2023.36.3.173

Kong, S., Moon, J., Song, J.K. (2022) System-Level Seismic Fragility Evaluation of Bridge Considering Aging Effects, J. Comput. Struct. Eng. Inst. Korea, 35(3), pp.149~158. 10.7734/COSEIK.2022.35.3.149

Lee, J., Cha, K., Song, S., Kong, J.S. (2015) Visualization Technology of GIS Associated with Seismic Fragility Analysis of Buried Pipelines in the Domestic Urban Area, J. Comput. Struct. Eng. Inst. Korea, 28(2), pp.177~185. 10.7734/COSEIK.2015.28.2.177

Lee, S., Yi, W., Kim, H. (2014) Seismic Fragility Functions for Steel Moment Resisting Frames using Incremental Dynamic Analyses, J. Comput. Struct. Eng. Inst. Korea, 27(6), pp.149~ 158. 10.7734/COSEIK.2014.27.6.509

Lee, S., Yoon, S., Song, H., Lee, J., Lee, Y. (2023) Comparative Study on Seismic Fragility Curve Derivation Methods of Buried Pipeline Using Finite Element Analysis, J. Earthq. Eng. Soc. Korea, 27(5), pp.213~220. 10.5000/EESK.2023.27.5.213

MLIT (2018) Korea Seismic Design Standard (KDS 17 10 00), Ministry of Land, Infrastructure and Transport, Sejong-si, Korea.

Park, H.S., Nguyen, D., Lee, T. (2016) Seismic Fragilities of Bridges and Transmission Towers Considering Recored Ground Motions in South Korea, J. Earthq. Eng. Soc. Korea, 20(7), pp.435~441. 10.5000/EESK.2016.20.7.435

Shinozuka, M., Feng, M.Q., Lee, J., Naganuma, T. (2000) Statistical Analysis of Fragility Curves, J. Eng. Mech., 126(12), pp. 24~31. 10.1061/(ASCE)0733-9399(2000)126:12(1224)

Somerville, P., Smith, N., Punyamurthula, P., Sun, J. (1997) Development of Ground Motion Time Histories for Phase 2 of the FEMA/SAC Steel Project, SAC Joint Venture, Report No. SAC/BD-97/04.

Yi, S., Papaknstantinou K.G., Andriotis C.P., Song, J. (2021) Appraisal and Mathematical Properties of Fragility Analysis Model, The 13th International Conference on Structural Safety and Reliability (ICPSSAR),Sanghai, P.R. China.

Journal of the Computational Structural Engineering Institute of Korea 한국전산구조공학회 논문집 ISSN:1229-3059(Print) 2287-2302(Online)

Preview

Seismic Fragility Analysis of Single-Degree-of-Freedom Model Based on Input Earthquake Ground Motions in Strong and Low-to-Moderate Seismic Regions

ABSTRACT

MAIN

Table 1

List of domestic earthquake and overseas intra-plate earthquake record set (Kim et al., 2016a, 2016b).

Table 2

List of FEMA P-695, Far-Field record set (FEMA, 2009)

Table 3

List of SAC steel project, Near-Fault record set (Somerville et al., 1997)

Fig. 1.

Push-over curve for bi-linear SDOF in natural period 0.5s

Table 4

Nonlinear SDOF parameters for three natural periods

(1)

Table 5

Definition of damage states (DS) level

Table 6

Damage Threshold displacement of damage states for three natural periods

Fig. 2.

Average acceleration response spectrum for four sets of input earthquake ground motions

Table 7

Spectral Acceleration of four sets for three natural periods

Fig. 3.

Seismic Fragility curves at damage state level 1

Table 8

Seismic fragility parameters and results of damage state 1 (DS 1) in natural period 0.15s

Table 9

Seismic fragility parameters and results of damage state 1 (DS 1) in natural period 0.5s

Table 10

Seismic fragility parameters and results of damage state 1 (DS 1) in natural period 1.0s

Fig. 4.

Seismic Fragility curves at damage state level 2

Table 11

Seismic fragility parameters and results of damage state 2 (DS 2) in natural period 0.15s

Table 12

Seismic fragility parameters and results of damage state 2 (DS 2) in natural period 0.5s

Table 13

Seismic fragility parameters and results of damage state 2 (DS 2) in natural period 1.0s

Fig. 5.

Seismic Fragility curves at damage state level 3

Table 14

Seismic fragility parameters and results of damage state 3 (DS 3) in natural period 0.15s

Table 15

Seismic fragility parameters and results of damage state 3 (DS 3) in natural period 0.5s

Table 16

Seismic fragility parameters and results of damage state 3 (DS 3) in natural period 1.0s

Fig. 6.

Seismic Fragility curves at damage state level 4

Table 17

Seismic fragility parameters and results of damage state 4 (DS 4) in natural period 0.15s

Table 18

Seismic fragility parameters and results of damage state 4 (DS 4) in natural period 0.5s

Table 19

Seismic fragility parameters and results of damage state 4 (DS 4) in natural period 1.0s

Acknowledgements

References